Detectives Juan Mir Pieras of Spain and Normand Laliberté of Ontario have clearly established that Descartes is guilty; he lied when he claimed to have seen Abel.
In the following diagram each professor is represented by his initial. He is joined by an arrow to each professor that he claimed to have seen. We know that
- each professor entered the room just one time, and
- when two professors were in the room together, at least one of them noticed the other (as summarized by the arrows in the diagram), and
- one or possibly two of the arrows represent a lie and should not be there.
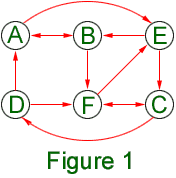
Solution by Laliberté.
It is certain that Abel and Bernoulli were in the room at the same time: each said he saw the other and at most one of these claims could be false. Likewise, it is certain that Cauchy and Fermat were in the room together. On the other hand, Abel and Cauchy were never together in the room since neither noticed the other. (Similarly, Abel and Fermat were never together.) Thus the interval of time AB (the time when Abel-Bernoulli were together) is disjoint from CF (the time Cauchy and Fermat were together). For convenience we shall discuss only the case in which AB precedes CF; the other case uses the same argument.
Since
Abel claimed to have seen Erdös, who claimed to have seen Bernoulli, and
Fermat claimed to have seen Erdös who claimed to have seen Cauchy,
we may conclude that Erdös arrived before the last of Abel and Bernoulli departed, and he left only after the first of Cauchy and Fermat arrived. We are therefore certain that the correct sequence of events must have been
- Bernoulli entered,
- Abel left,
- the first between Cauchy and Fermat arrived,
- Erdös left.
We next argue that Descartes could have entered the room only after these events. Indeed, Cauchy claims to have seen Descartes, who claims to have seen Fermat. Thus Descartes is there during the visit of Cauchy or Fermat, but not during the visit of Bernoulli or Erdös. Since Descartes could not have left before Bernoulli entered (by condition (3)), he must have entered after Bernoulli left. However, we have observed that at the time when Bernoulli left, either Erdös was already present or Abel was still there. In the former case Descartes could not enter until Erdös had left, while in the latter case Erdös was entering before Abel left — in particular, before the first of Cauchy and Fermat entered. In any case, Descartes was entering only after the departure of Erdös, but while Cauchy or Fermat still were there. We then conclude that Descartes could have arrived only after Abel had left. He was therefore lying when he said that he had seen Abel.
Solution by Mir.
Let us say that a visual contact is established between two professors when they are in the room at the same time and at least one of them has seen the other. Mir has interpreted the problem to be that we are given a list of ten visual contacts, of which nine are true and one is false.
When three professors are in the room at the same time the result is necessarily a visual triangle — there is a visual contact between each pair of them. Our list contains four visual triangles:
Bernoulli-Erdös-Fermat,
Cauchy-Descartes-Fermat, and
Cauchy-Erdös-Fermat.
Four professors in the room at the same time would result in a visual tetrahedron. However, our list of visual contacts (which, you recall, has no omissions) contains no visual tetrahedron. Consequently, no more than three professors could be in the room at the same time.
Let us enumerate the visual contacts by giving a credit to the second of each pair to enter the room. (Of course, the person we credit might not be the person who claimed the sighting.) In particular, the first professor to enter that morning will not receive any credit, while the second gets at most one. The others, from the third to the sixth, each have at most two visual contacts to their credit since no four of them are ever in the room together. Thus, the only way to obtain a total of nine visual contacts is to give one credit to the second professor to enter and two contacts to the credit of each subsequent professor. It follows that each professor after the second creates a visual triangle upon entering the room, for the maximum of four. Thus the four visual triangles listed above must all be authentic. The false visual contact can only be the unique contact not contained in one of these triangles: Descartes lied in claiming to have seen Abel.
Comments. Suppose that the time when each professor was in the room is as follows:
Bernoulli from 9:20 to 10:40
Cauchy from 11:00 to 12:00
Descartes from 11:40 to 12:40
Erdös from 9:40 to 11:20
Fermat from 10:20 to 12:20
We can illustrate this information by representing each professor by his initial, and joining pairs of these by a line if the times they were in the room overlap.
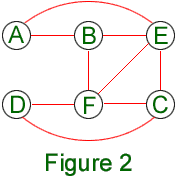
We call such a diagram an interval graph: The letters (or vertices) correspond to time intervals, and the edges join the intervals that overlap. Note that the first diagram (with arrows instead of edges) had a connection from D to A. The solution to the problem comes down to the observation that the first graph is not an interval graph. Indeed, the induced configuration of 4-cycles, like the example WXYZ below, is impossible in an interval graph: Intervals W and Y
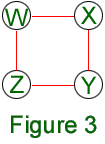
have no overlap; should W precede Y then both X and Z would have to overlap the end of W and the beginning of Y. This would imply that X and Z should overlap, so they would have to be joined by an edge.
In the first diagram one sees three induced 4-cycles: ADFB, ADFE, and ADCE. The guilty person would have to be included in each of these 4-cycles, and moreover the removal of his lie (or lies) would have to break all these 4-cycles. Once again we conclude that the only possibility is that Descartes lied in claiming to have seen Abel.
The idea of using interval graphs in detective stories was exploited in depth by Claude Berge in his novelette Que a tué le Duc de Densmore? (Who Killed the Duke of Densmore?, Bibliothèque Oulipienne No. 67). The story presented here is taken from Introduction to Graph Theory by D. West. It originally appeared in Algorithmic Graph Theory and Perfect Graphs by M.C. Golumbic.