You are given a 2ⁿ by 2ⁿ grid of squares, and uncle Albert places a penny on one of them.

Your job is to cover the remaining 2²ⁿ – 1 squares with (2²ⁿ – 1)/3 trominoes. Can you do it?

Solution to MP29

We received complete solutions from Francesco Barioli (Regina), Pierre Bornsztein (France), Normand LaLiberté (Quebec), Juan Mir Pieras (Spain), Gordon Robinson (British Columbia), Jayavel Sounderpandian (Wisconsin), and Jason Stein (Regina), and special cases from Rachel Fello (internet) and Lina (California). Most of the complete solutions were quite similar in the way they used mathematical induction. Those readers who are unfamiliar with the way induction works can consult our Math Central Resource Room page
http://mathcentral.uregina.ca/RR/database/RR.09.95/nom3.html.

Our first solution combines the work of Robinson, Sounderpandian, and Stein. (See our French and Spanish web pages for other solutions.) We follow it with Barioli's solution, which uses a different form of induction, one that allows us to investigate the problem of covering m by n grids.

First solution
We want to show that by removing a square from a 2ⁿ by 2ⁿ grid of squares, the remainder can be covered with (2²ⁿ – 1)/3 trominoes.

The case n = 1. We simply observe that when the penny is placed anywhere on a 2 by 2 grid, the remaining three squares form a tromino, so those squares are automatically covered by a tromino.

The case n = k. Now suppose the problem is solved for all n < k and consider the case n = k. Place the coin on any square, and divide the grid into 4 quadrants each 2k-1 on a side. The coin must be in one of these quadrants. By induction (our assumption) we know how to solve the problem for this quadrant since (k-1) < k, and so we can cover this quadrant, except for the coin, with trominoes. This leaves the remaining three quadrants. Place a tromino in the corner formed where all three quadrants meet so that the tromino covers one square from the corner of each of the three quadrants. (The figure shows the

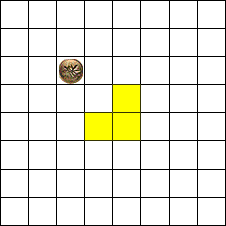
case for n=3, with the coin in the northwest quardrant and a tromino covering one corner of each of the other three.) Now what remains are three square grids (side 2^k-1) with one square already covered. So by induction, we can cover the remainder of each quadrant grid with trominoes. Note that the number of trominoes used is

Since we have now covered the whole grid except the coin, the proof is completed. Mathematical induction guarantees that the statement is true for all n.

Here is Fello's picture of the 4 by 4 case featured in the statement of our problem.

Barioli's solution.
Barioli's way of looking at the problem is different from the others. He defined a 2²-square as a 2ⁿ by 2ⁿ grid of squares, and a 2ⁿ-tromino as the "fat" L-shaped tromino formed by joining three 2^n-1-squares. The usual tromino is then a 2¹-tromino; of course, a 2ⁿ-square is formed by joining a 2^n-1-square to a 2ⁿ-tromino.

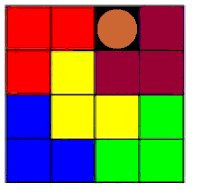
The following picture shows us that a 2ⁿ-tromino can be covered by four 2^n-1-trominoes. By induction we conclude that a 2ⁿ-tromino can be covered by a suitable number of 2¹-trominoes.

So, after Uncle Albert has placed his penny on a 2ⁿ-square, here is a simple way to cover the remaining squares of the grid.

1. Split the 2ⁿ-square into a 2ⁿ-tromino plus a 2^n-1-square in such a way that the 2^n-1-square contains the penny.
2. Cover the 2ⁿ- tromino with 2¹-trominoes
3. Apply step 1. to the 2^n-1-square, replacing n with n–1, until you arrive at a 2¹-square.

Since a 2¹-square can be covered with a 2¹-tromino no matter where the penny is placed, we conclude that it is always possible to cover a 2ⁿ-square.

Remark 1. The covering strategy is unique only for n = 1, 2.

Remark 2. It is natural to wonder what happens with an m by n rectangular grid: place a penny on one of the mn squares; if mn – 1 is divisible by 3, can the remaining squares of the grid be covered with (mn – 1)/3 trominoes? Barioli has an argument that requires looking at many special cases and reducing each to a smaller case (much as in his argument above). It seems that with a little patience one can prove that there are only a few types of m-by-n rectangles that one cannot cover. Indeed, the impossible cases fit into four classes. Barioli's claim is that when m ≤ n and 3 divides mn – 1, the task is possible for all grids except the following four types.

1. m = 1.
2. m = 2, n = 5 + 3k, k ≥ 0, and the penny placed in the following position (where k' + k'' = k):
   
   
   
3. m = 5, n = 8 + 3k, and the penny in the middle row, two columns from the end:
   
   
   
   
4. m = n = 5, and the penny in anyone of the following 16 positions: