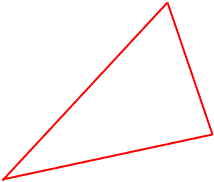
Given a triangle and an infinite blue and white checkerboard, show that the triangle can be placed on the board with all its vertices strictly in the blue.
Solution to MP33
We received correct solutions from Pierre
Bornsztein (France),
Patrick J. LoPresti (USA), and Juan Mir Pieras (Spain). We found the
problem in Siam Review 13:1 (January 1971), p. 115; 14:4 (October 1972),
p. 647.
D.J. Newman (Yeshiva University) both posed the problem and provided
its solution. A solution is not very hard; what is hard is putting
the solution
into words. Mir avoided this difficulty by putting his solution into
pictures.
First, the solution in the combined words of Bornsztein and Newman.
Let us assume
that the cells of the checkerboard are unit squares,
oriented so that the sides are horizontal and vertical. (If you prefer,
you may introduce coordinates so that the corners of the squares are
those points with two integer coordinates.) Place vertex A of our triangle
ABC at a corner of one of the squares, then rotate it so that
-
no other vertex is on a side of any square, and
-
the lengths of the orthogonal projections on the horizontal
and the vertical lines of the board are not integers.
(Bornsztein was careful to point out that there are only
finitely many
orientations of the side BC where a projection has integer length, while
there are infinitely many that satisfy conditions (1) and (2).
Next, translate the triangle horizontally
until B is on a vertical line. Our initial rotation insures that neither
A nor B is at a
corner of
a square, while C is interior to a square. Therefore, a slight motion
vertically and a slight motion horizontally will not change the colour for
C, but they can independently reverse the colours of the other two vertices.
Thus,
one easily gets the three vertices into the interior of squares of the same
colour. If that colour is blue, then our task is
complete; if white, then translate the triangle up one unit.
Lo Presti began differently. He made use of the fact that all points along a diagonal of the blue squares are blue except the corners. If you slide side AB along a blue diagonal, then there will be a position where C lies inside a blue square except in the annoying case where C moves along a white diagonal. It is not too difficult to dispose of that annoying case.
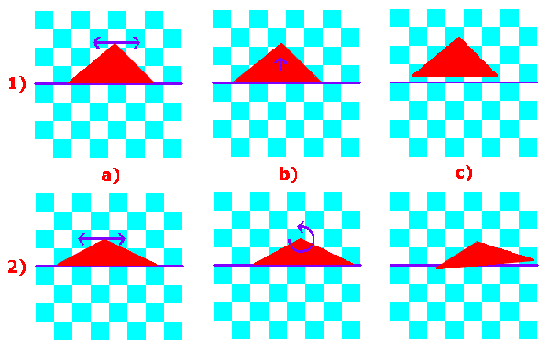
Finally, here is Mir's argument.
Note that it is similar in spirit to our
initial verbal argument,
but he requires two cases.