(a) Given a set of points in the plane such that
- the distance between any two of them is an integer, and
- infinitely many of them lie on the same line,
(b) What happens if we ask only that 5 points lie on the same line?
We received solutions from Pierre Bornsztein (Pontoise, France), Steve Brooke (Vancouver), Juan Mir Pieras (Spain), and Jacob Tsimerman (Toronto).
Two proofs of (a).
Let us denote the given set by S, and call l the line that contains infinitely many points of S. All solvers began by supposing, contrary to the claim in (a), that there is a point P of S not on l. Let F be the foot of the perpendicular from P to l. Along the line
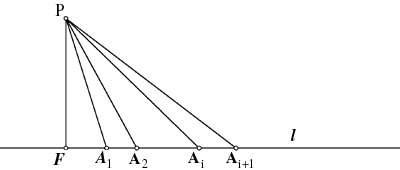
on at least one side of F there must be infinitely many points of S; denote these points A1, A2, ... , in order of increasing distance from F. Because PAi is a positive integer for all i, PAi+1 >= PAi + 1. As a consequence, the distance PAi grows without bound as i goes to infinity. We need one more preliminary fact (from Bornsztein): the distances FAi must all be rational. To see this, note that
| PA22 | = | PF2 + FA22 |
| = | PF2 + (FA1 + A1A2)2 | |
| = | PF2 + FA12 + 2(FA1)(A1A2) + A1A22 | |
| = | PA12 + 2(FA1)(A1A2) + A1A22 |
Since all distances except possibly FA1 in the last equation are integers, FA1 must be rational; namely,
We can now modify the given configuration by turning all these given rational distances into integer distances: Dilate the configuration by the factor 2A1A2; then FA'1 := 2(A1A2)(FA1) is an integer, and therefore all distances FA'i := 2(A1A2)(FAi) from F to the image of Ai under the dilatation will be integers. We can therefore simplify our proofs of (a) by assuming, without loss of generality, that we are given from the start that FAi and PAi are integers for all i.
Bornsztein's solution to (a) follows quickly from these observations. We note that since PAi and FAi are both integers, while the former is the hypotenuse and the latter a leg of a right triangle, PAi - FAi >= 1. Therefore,
| PF2 | = | PAi2 - FAi2 |
| = | (PAi + FAi)(PAi - FAi) | |
| >= | (PAi + FAi) | |
| >= | PAi |
From this inequality we conclude that if P were a point of S not on l, PAi would be bounded by PF2 (the square of the distance from P to l), which contradicts the fact that it is unbounded. It follows that there can be no such P: all points of S must lie on l. This completes the first proof.
Our preliminary observations also suggest that we can prove a generalization of a familiar theorem about Pythagorean triples: For any positive number d there are finitely many right triangles having one leg of length d, while the lengths of the other leg and hypotenuse are both integers.
Here is the proof supplied by Tsimerman and suggested by Brooke. Let d = PF and x = FA for some A in the given set S on the line l. We want to show that we can choose i so that it is not possible for 
to be an integer for any i for which FAi > FA. First, note that
We want our x large enough so that 
-- in this way PA would be trapped between consecutive integers so that it could not be an integer. Squaring both sides of this last inequality, we get d2 <&nnbsp;2x + 1, or x > (d2 - 1)/2. Putting this all together, we conclude that for any i for which FAi > (d2 - 1)/2, PAi could not be an integer:
Thus, there can be at most finitely many of the PAi that are integers. This argument therefore gives us an alternative proof of part (a), that all points of S are on line l. (Otherwise there would exist the point P not on l that would determine F at the foot of the perpendicular, and there would be at most finitely many integer distances PAi contrary to the initial assumption that there are infinitely many.)
Bornsztein notes further that our problem is a special case of a theorem of Anning and Erdös:
We seek a 6-point set for which the distances between pairs of the points are all integers, while 5 of the points lie on a single line and one point is not on that line. Bornsztein, Mir, and Tsimerman all use integer-sided right triangles having one leg of length 12 -- there are four of them to choose from: (12, 5, 13), (12, 9, 15), (12, 16, 20), and (12, 35, 37). For example, let (0, 12) be the coordinates of the outside point, and (0, 0), (9, 0), (-9, 0), (16, 0), and (-16, 0) be five points on the line y = 0.
Mir provided a simple way to construct a finite set S having any number k+1 points on a line and one point off the line, with an integer distance between any two of its points. His idea is based on the familiar set of Pythagorean triples (2mn, m2 - n2, m2 + n2) -- these triples have the property that for any integers m and n with m > n, the sum of the squares of the first two is the square of the third. In other words, these triples represent the sides of integer-sided right triangles. Let the first member of the triple be N = 4k = 2.22k-1.20 = 2.22k-2.2 = 2.22k-3.22 = ... = 2.2k.2k-1. We have factored N into k different ways of writing the product 2mn, and we can therefore create k different Pythagorean triples. This leads to a set S of k+2 points, consisting of (0, 4k), (0, 0), and the points (m2 - n2, 0) corresponding to the third vertices (4k - 4k-1, 0), ..., (42k-2 - 40, 0) of the k integer-sided right triangles.
Of course, there is a simple way to list and to count all Pythagorean triples. Brooke referred to the informative Mathworld web page:
Type Pythagorean triples (or any other topic of interest) where it says "search." There you will learn that if the integer a is not congruent to 2 modulo 4, and the number of its distinct prime factors is n, then there are precisely 2n - 1 primitive Pythagorean triangles having a as the length of one of its legs. (Here the word primitive means that no two of the side lengths of the triangle have a common factor). On the other hand, there exists no primitive Pythagorean triple whose even member is 2 modulo 4.