In stores one finds perpetual calendars that consist of a pair of cubes whose faces each show a number from 0 to 8. The numbers are arranged so that the two blocks can be placed together to represent all 31 days of a month. One block has the numbers 0 through 5 on its faces, while the other has the numbers 0, 1, 2, 6, 7, 8. It is obvious that the numbers 0,
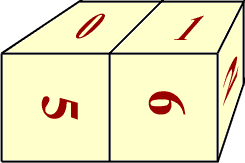
1, and 2 must appear on each block (to accommodate the single-digit days and also days 11 and 22). But what about 9, 19, and 29? One needs here the trick that the face numbered 6 serves also for 9.
It is said that we use a base-10 system for counting because we have ten fingers. Our problem for this month is to use numbers in bases other than 10 to design calendars for people with fewer than ten fingers. In particular,
-
can you place base-2 numbers on each of the 12 available faces on the two cubes to produce all numbers from 1 to 31 (= 111112)? If you do it economically there will be faces left over to accommodate advertising?
-
is it also possible using base 9?
What are base-2 numbers, you ask? Their story is told on the Mathworld web page,
On that page you will find the numbers form 1 to 30 written in base-2 notation.
We received solutions from Wolfgang Kais (Germany), and Matthias Nurnberger (massmed.org), two solutions from Patrick LoPresti (USA), and two solutions from Normand Laliberté (Ontario). All the solutions were different! Each had a nice aspect to it, so let’s look at them all together in order to compare them.
Solution to MP37
| First die | Second die | |
| Kais | 00, 01, 11 | 000, 001, 010, 011, 101, 111 |
| Variation on Kais | 00, 01, 11 | 01, 11, 100, 101, 110, 111 |
| Laliberté 1 | 00, 01, 11 | 001, 010, 011, 101, 111 |
| Laliberté 2 | 0, 1, 0001, 0010, 0011, 0101 | 0,1, 0111, 1011, 1111 |
| LoPresti | 000, 001, 010, 011, 100, 101 | 00, 01,10,11, 110, 111 |
| Nurnberger | 0,1, 11, 100, 101 | 0, 1, 10, 11, 110 |
Laliberté was the clear winner – he needed only eight faces, so there are four left over for advertising. The people who publicize Viagra would certainly get very excited about the prospect! His plan 1 is the same as Kais’s, except he managed without the face with 000. The advantage of using the redundant 000 is that one sees instantly that it works: you get the numbers 1 through 7 using the triple digits of die 2 in back with 00 in front, 8 through 15 with 01 in front, 16 through 23 with 10 in front (which is 01 turned over), and 24 through 31 with 11 in front. Laliberté noticed that you can live without the 000 using (010)(00) for 8, (100)(00) for 16, and (110)(00) for 24.
LoPresti decided that since the symbol for one is asymmetric in all of his fonts, he should manage without using symmetry -- at the risk of upsetting the advertisers (because he needed all 12 faces).
Nurnberger solution offers nice symmetry, using five faces per die, but he was forced to resort to an interesting subterfuge! He combined the base-2 symbols with our base-10 system to write numbers like 16 as (1) followed by (110) (which is the symbol for 6). That’s not really a base-2 representation of 16 (which is10000 in base 2), but since the rules of the game were a bit vague, the cleverness of the solution overcame the objections from the purists.
One easily checks the correctness of the other solutions (remembering that faces like 01 serves also for 10, except in LoPresti’s solution). Here are the base 2 numbers from 1 to 31. One just has to check that each base-2 number can be represented with one face from each die of a proposed solution.
| 1 | 1 | 9 | 1001 | 17 | 10001 | 25 | 11001 | |||
| 2 | 10 | 10 | 1010 | 18 | 10010 | 26 | 11010 | |||
| 3 | 11 | 11 | 1011 | 19 | 10011 | 27 | 11011 | |||
| 4 | 100 | 12 | 1100 | 20 | 10100 | 28 | 11100 | |||
| 5 | 101 | 13 | 1101 | 21 | 10101 | 29 | 11101 | |||
| 6 | 110 | 14 | 1110 | 22 | 10110 | 30 | 11110 | |||
| 7 | 111 | 15 | 1111 | 23 | 10111 | 31 | 11111 | |||
| 8 | 1000 | 16 | 10000 | 24 | 11000 |
LoPresti's explanation provides a lovely motivation for the solution of Kais, as well as his own first solution. He first solves the problem for base-8 cubes (with days numbered from 01 to 37), using the digits 0,1,2, and 3 on both cubes, 4 and 5 on die 1, and 6 and 7 on die 2. The next step is to change these symbols into their base-2 equivalents:
Cube 1a: 000, 001, 010, 011, 100, 101
Cube 2a: 000, 001, 010, 011, 110, 111
For days in the form 8n + 6 or 8n + 7, we put die 1 first; for the other days, we put die 2 first. To make room for advertising, we can make use of symmetry. Our rule tells us that faces 000, 001, 010, and 011 on Cube 2a are only used when Cube 2a is placed first. Thus, we can instead label them 00, 01, 10, and 11, which is useful because 01 and 10 occupy only one face (by symmetry).
So we can replace our cubes with
Cube 1b: 000, 001, 010, 011, (100), 101, (110), 111
Cube 2b: 00, 01, (10), 11
The numbers in parentheses already appear
as the reverse of
another number on the same cube. This
leaves us three faces for advertising, all on Cube 2b.
Our new rule is that Cube 2b always appears first, which is a nice
property. Finally, if the redundant leading zeroes annoy us, we
can replace Cube 2b with:
Cube 2c: 0, 1, 10, 11
This step would leave us only two faces for advertising, but that is still pretty good.
The answer to part (b) is that we cannot use base-9 numbers for our perpetual calendar. This is simply a limitation of our notation: One would imagine that base-9 counting would be invented by an alien race of individuals having three hands, each with three fingers, and that their symbols would be different from ours. The impossibility of a base-9 labeling is a consequence of needing the digits 1, 2, and 3 on each die for the days 11_9, 22_9, and 33_9 (days 10, 20, and 30). Each die must also have a face 0 to combine with the single-digit dates 1 through 8. That leaves four faces to fit the five remaining numbers 4, 5, 6, 7, and 8. There is no digit 9 that can be flipped into a 6, so, like our friends from that alien race, we’re stuck with a missing digit.
Our December problem is based on an idea of Jeroen Doumen, a student at the Technical University of Eindhoven.