We received solutions this month from Pierre Bornsztein (France), Gilles Feyrit (France), Wolfgang Kais (Germany), Juan Mir Pieras (Spain), and Patrick LoPresti (USA).   Their methods were quite similar but, as we shall see, there are interesting variations in the details.

Solution to MP39

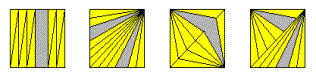
Solution to Part (1) .

            There are many ways to dissect a square into an even number of equal-area triangles.   Most of the methods we received are based on the idea of forming n triangles that have equal base and equal height.   Mir sent us a diagram showing three ways of doing this: by cutting into n/2 equal segments a pair of opposite sides, or a pair of adjacent sides, or a diagonal.   His final diagram shows that one can mix methods - half the triangles have base and height , while the other half have base 2/n and height 1.

 

Solution to Part (2) .

            We are given a square and wish to cut it into three triangles.   Let us call this a 3-dissection .   All submitted solutions showed more than what was required:

Theorem. For any 3-dissection of a square, the area of one triangle will necessarily be half the area of the square.

Of course, this theorem immediately implies the desired result - the areas of the three triangles of any 3-dissection could never be equal; in fact, the area of the big triangle will equal the sum of the other two.   We begin with some preliminary observations that were common to most of the submitted solutions.

Observation 1 .   The vertices of the triangles of any 3-dissection of a square come from a set of five points - the vertices of the square plus one further point P.   Moreover, P must lie properly on either a side of the square, or a side of one of the triangles.

Proof . The angles of the triangles sum to 3 180^o .   These angles must fill the angles of the square, which account for only 2 180^o.   The remaining 180^o calls for a further point to serve as a vertex.   Were that point in the interior of the square, the angles about it would sum to 360^o (which would be too much), unless the point lay on a side of a triangle without being a vertex of that triangle.

Observation 2 .   Each triangle of any 3-dissection shares at least two of its vertices with the square.

Proof .   This is an immediate consequence of observation 1 - A triangle with a vertex at P must share its other two vertices with the square because there are no other points available.

Proof of the theorem by Bornsztein, Feyrit, and LoPresti.

            Our observations tell us that at least two triangles will have a vertex at the new point P; thus, at least three vertices of the square will be used for the other vertices of these triangles.   Let two of them be the vertices A and B of the square ABCD.   Where can P lie?

Case (a). P can lie on the segment CD, in which case D ABP has area half the square (with base AB and height equal AD = BC = (distance from P to AB).

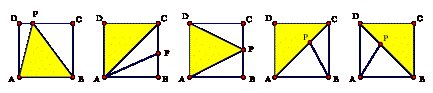
Case (a)

Case (b) (and (c))

Case (d)

Case (b). P can lie on the segment BC.   Then quadrangle APCD must be dissected into two triangles.   One must therefore cut either along the diagonal AC or along the diagonal DP.   The big triangles will be, respectively, D ACD and D APD.

Case (c). P can lie on the segment AD (not shown in the figure).   By symmetry this case is essentially the same as case (b) (exchanging B with A and C with D)- the big triangles will be D BDC and D BPC.

Case D.   P can lie inside the square. By observation 1, P must lie on a side of one of the triangles; that side (joining two vertices of the square) can only be AC or BD.   In the first instance D ACD has area half the square; in the second, it is D BCD.   This completes the theorem's proof.

Remark .   A couple of our solvers claimed that a pentagon could not be dissected into fewer than three triangles.   One must be more careful here.   The claim is certainly true for convex pentagons (with all angles less than 180^o), but it is not true of the pentagon APBCD that appears in case (d), as can be seen in the diagram.

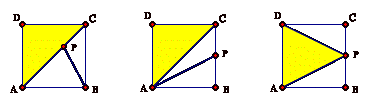
Proof of the theorem by Mir .  

            From observation 2 each triangle shares at least two vertices with the square.   Without loss of generality, one triangle will share edge AB with the square and another will share DA.   As shown in the diagrams, the third will share with the square vertices B and C, A and C, or C and D.   In each case the area of the yellow triangle is half that of the square.

Proof of the theorem by Kais .

Case (a).   If P is not an interior point of a side of the square, then every side of the square is shared with one of the triangles.   Because there are three triangles but four sides, two of these sides must belong to the same triangle.   Because these two sides cannot be parallel, they must be adjacent.   The third side of the triangle would then have to be a diagonal of the square, so that triangle fills half the square.

Case (b).   If, on the other hand, P is an interior point of a side of the square, say BC, then by our observation 1, the other three sides of the square are shared with the triangles.   In particular, the triangle whose side is AD (opposite P) must have its third vertex on the side BC (at C, at P, or at B, as in case (b) of the first proof).   Again its area equals half that of the square, and the third proof is complete.

Comments on extensions of the problem.

            Good problems always lead to further problems.   What about a dissection of the square into 5, 7, or an arbitrary odd number of equal-area triangles?   Mir did not try to answer this question, but he showed that if there were a way to dissect a square into n triangles of equal area, then it could also be done for n+4 triangles and, therefore by induction, for n + 4k triangles.   Here is how he did it.   If n+4 triangles are wanted and the square has side s , each triangle will have area s 2 /(n+4).   The figure shows how to partition the square into four right triangles whose base is a side of the square (of length s) and height is 2s/(n+4), together with one square that by hypothesis can be divided into n equal-area triangles.   (The vertices of the 4 triangles that lie inside the outer square are the points where the appropriate height line intersects the circle whose diameter is a side of the square; this produces the required right angles.)

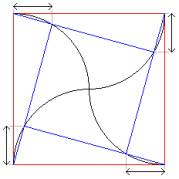
            Since it is possible to dissect a square into two or four equal-area triangles (using one or two diagonals, respectively), we can produce 2 + 4k or 4 + 4k triangles and have yet another way of answering part 1 of the monthly problem.   Should it be possible to dissect the square into an odd number of triangles for some n, then Mir's observation would lead to dissections for infinitely many possible odd numbers.

The question of dissecting a square into an odd number of triangles of equal areas seems first to have been raised by Fred Richman in 1965.   His colleague John Thomas answered it in part; Paul Monsky ( American Mathematical Monthly 77 :2 (February 1970), 161-164), building on Thomas's work, showed the answer to Richman's question is

There is no dissection of a square into an odd number of triangles of equal area .

  Although his argument is not elementary, it is not very difficult.   The story is told in an elementary way by Sherman Stein in a paper that appeared, by coincidence, just last month: "Cutting a Polygon into Triangles of Equal Areas,"   The Mathematical Intelligencer , 26 :1 (2004), 17-21.   Stein also discusses a number of related dissection problems involving various shapes in the plane and in higher dimensions.   Some of those problems have not yet been solved.   We are grateful to Pierre Bornsztein for informing us of the Stein reference.