Here is another dice problem for the holiday season. With an ordinary pair of dice the sum distribution is

Possible sums	2	3	4	5	6	7	8	9	10	11	12
distribution of sums	1	2	3	4	5	6	5	4	3	2	1

The table tells us that the sum 2 appears in one way (as 1 + 1), 3 appears in two ways (as 1+2 and as 2+1), and so forth. The problem for January is to find another way to put numbers on the dice with the same sum distribution.

We thank Ed Doolittle of the University of Regina for suggesting our January problem. He found it in A Problem Seminar, by Donald J. Newman (Problem Books in Mathematics, 1982), pages 18 and 98-99. Complete solutions were sent in by Gilles Feyrit (France), Wolfgang Kais (Germany), Normand Laliberté (Ontario), and Patrick LoPresti (USA). The last three came up with similar solutions, each with nice ideas that combine to form a really neat solution. Feyrit took quite a different approach: he used polynomials. In addition we received from Andreas Schüller (Germany) a nice way of describing one of the two infinite families of solutions.

Solution to MP38

We begin with the direct approach.

I. The combined solution of Kais, LaLiberté, and LoPresti, with an idea from Schüller.

Our problem is to devise a pair of dice with the same distribution of outcomes as ordinary dice. Specifically, we want the outcomes displayed in the top row of the table to occur the number of times displayed in the bottom row.

Possible sums	2	3	4	5	6	7	8	9	10	11	12
Desired frequency	1	2	3	4	5	6	5	4	3	2	1

Although we did not require it explicitly, we may as well assume that the numbers on the faces of our dice are represented by dots, and are therefore positive integers. We could also allow fractions or negative numbers, but

Observation. If a pair of dice provides a solution to our problem, then so does a second pair obtained from the first by adding a fixed number x to each face of one die and subtracting x from each face of its mate.

For the sum 3 to occur twice we must have two 2s, either with one 2 on each die or both 2s on one die. We consider the cases separately.

Case 1. Suppose that r₂ = g₂ = 2.

For a sum of 4 to happen three times in this case, we need two 3s (since we already have one 4 with 2+2). These could both be on one die, say the red one, or there could be one 3 on both dice. We shall now eliminate the first possibility.

Possibility 1a: r₃ = r₄ = 3. Our assumptions at this point leave us with the possibility

Red die	1	2	3	3	r5	r6
Green die	1	2	g3	g4	g5	g6

We now have two sums of 5 and need two more (which means we need two 4s), and no sum of 6 (because under our current assumption we may not use 3+3), so we need five more (which means three 5s are needed along with the two 4s). For our two 4s, because r₅ < r₆ they cannot both be on the red die; for the same reason we cannot have two red 5s, nor can we have two green 4s with two green 5s. Thus, one 4 goes on each die. Moreover, we cannot then have three green 5s (that would make g₅ = g₆). We are therefore forced to have one red and one green 4, and two green and one red 5:

Red die	1	2	3	3	4	5
Green die	1	2	4	5	5	g6

To make the largest sum a 12, we are now forced to set g6 = 7. Unfortunately, there are now the wrong numbers of many of the sums. (For example, there is only one 11 instead of two.) We conclude that possibility 1a is not possible after all: we cannot have both 3s on one die. We must have

Possibility 1b: r3 = g3 = 3. Thus case 1 definitely looks like this:

Red die	1	2	3	r4	r5	r6
Green die	1	2	3	g4	g5	g6

We can continue in this way to eliminate the possibility that both 4s are on one die (say (1, 2, 3, 4, 4, r6)), and finally conclude that

In case 1 we can have only the ordinary dice.

Here is a better approach, using a suggestion from Gilles Feyrit. His idea is based on an important problem-solving principle:

Always look for symmetry and for ways to exploit it.

In our problem the distribution of sums is symmetric about the central value of 7. This forces each die to be symmetric about its average value so that a sum of s above average occurs as often as a sum of s below average. Thus, symmetry here means that

(average of r₃ and r₄) = (average of r₂ and r₅) = (average of r₁ and r₆) = (average for the red die),

with a similar statement for the green average. Furthermore, the red average plus the green average must sum to 7. (Of course, one must prove such claims, but here the proof is without complications; we will leave it to the reader’s imagination.)

Let’s re-examine possibility 1a, this time using symmetry. Recall that we had assumed that there are two 3s on the red die: (1, 2, 3, 3, r₅, r₆). Symmetry forces the average red value to be (r₃+r₄)/2 = (3+3)/2 = 3, so its remaining faces would necessarily be r₅ = (ave + 1) = 4 (since r₂ = (ave – 1)), and r₆ = (ave + 2) = 5 (since r₁ = (ave – 2)). Thus the green die (1, 2, g₃, g₄, g₅, g₁) would need g₃ = 4 (to get the right number of sums of 5), and g₄ = 4 (to get the green average to be 4). But we already see that at this point 5 appears too often as a sum, so we at once have a contradiction. We conclude quickly that having both 3s on one die is not possible. We therefore are certain that in case 1 (with a 2 on both dice) 1, 2, and 3 must appear on both dice. To get the correct number of 5s at least one die would need a 4, say r₄ = 4. Symmetry now fixes everything! The average on the red die is necessarily (r₃+r₄)/2 = (3+4)/2 = 3.5, so that would necessarily be the average on the other die (to get an average sum of 7), and we are left with an ordinary pair of dice.

Case 2. Both 2s are on the same die.

Let’s put them on the red die, which is then (1, 2, 2, r₄, r₅, r₆). We now cannot use 2+2, so to get a sum of 4 three times we need three 3s. They cannot all be on the green die, because there would then be too many 5s. So r₄ = 3 and the average on the red die must be (r₃+r₄)/2 = (2+3)/2 = 2.5. The red die is therefore (using symmetry)

(1, 2, 2, 3, 3, 4).

The green die must have the third 3, so g2 = 3. We need one more sum of 5, so g3 = 4. Because 2.5 + (green average) = 7, we must have (g3+g4)/2 = 4.5; hence, g4 = 5. The green die must therefore look like

(1, 3, 4, 5, 6, 8).

At this point we know only that the dice must look like this if there is a hope of having both 2s on the same die. We must now check if the distribution that is forced upon us happens to be correct. By our construction we already know that the sums of 2, 3, 4, and 5 occur the right number of times. Because of symmetry it remains to check only that the sums of 6 and 7 have the right frequency. By good luck, they do! Listing the sums with the red value first we get

6 = 1+5, 2+4, 2+4, 3+3, 3+3, (so, five sums of 6);

7 = 1+6, 2+5, 2+5, 3+4, 3+4, 4+3, (so six sums of 7).

Our grand conclusion: There are two classes of solutions, case 1 (the ordinary dice)

red = (1, 2, 3, 4, 5, 6) and green = (1, 2, 3, 4, 5, 6),

and case 2 (the strange new dice)

red = (1, 2, 2, 3, 3, 4) and green = (1, 3, 4, 5, 6, 8).

Should you want to allow dice with blank faces, you get three more possibilities:

	Red	Green
From case 1	(0, 1, 2, 3, 4, 5)	(2, 3, 4, 5, 6, 7)
From case 2	(0, 1, 1, 2, 2, 3)	(2, 4, 5, 6, 7, 9)
	(2, 3, 3, 4, 4, 5)	(0, 2, 3, 4, 5, 7)

Finally, if you wish to allow arbitrary real numbers on the faces, you can get further examples by adding the same number to each face of one die of a basic solution, and subtracting that number from each face of the other.

II. Solution by Gilles Feyrit Generating functions.

The starting point for this approach is the observation that the numbers on the faces of a pair of dice add together like the exponents of polynomials under multiplication. In fact, in combinatorics it is often useful to reduce a problem involving counting combinations to a problem of factoring polynomials. These polynomials are called generating functions. The idea here is simple: the red die with its face numbers r₁ ≤ r₂ ≤ ... ≤ r₆ is represented by the polynomial r = x^r₁+x^r₂+...+x^r₆; the green die with its faces g₁ ≤ g₂ ≤ ... ≤ g₆, by the polynomial g = x^g₁+x^g₂+...+x^g₆. For ordinary dice the corresponding polynomials equal one another,

r = g = x + x² + x³ + x⁴ + x⁵ + x⁶.

When you multiply them together, the coefficients appearing in the product are easily recognized as giving the distribution of outcomes from rolling a pair of dice:

r·g = x² + 2x³ + 3x⁴ + 4x⁵ + 5x⁶ + 6x⁷ + 5x⁸ + 4x⁹ + 3x¹⁰ + 2x¹¹ + x¹²

Observe, for example, the coefficient 4 of x⁹ corresponds to the fact that an outcome of 9 occurs in four ways when dice are rolled.

Our goal is to find different polynomials r* and g* whose coefficients add up to 6 (because each die has 6 faces), and whose product r*·g* = r·g. (Observation: to get the sum of the coefficients just let x = 1 in the polynomial.) Consequently, we must find the factors of r and g that have integer coefficients. Here Feyrit used complex numbers to determine the possible factors. Alternatively, if you know that

1 + x + x² + x³ + x⁴ + x⁵ =

then the task is easy: r = g =

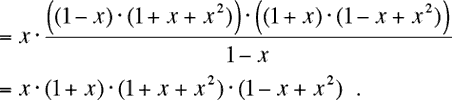
Thus

r·g = x²·(1+x)²·(1+x+x²)²·(1-x+x²)² = r*·g*.

Because of our earlier agreement that the smallest number on each die is a 1, each of r* and g* must have x as a factor. Since the sum of the coefficients in the factors (1+x), (1+x+x²), and (1 – x + x²) are respectively 2, 3, and 1, the only way to get sums of 6 is to use 1+x and 1+x+x² as factors in both r* and g*. Thus the only choice we have is where to put the two factors 1 – x + x². If one goes with r* and the other with g*, we are back to where we started. The other choice is to put them together -- in g*, say. Thus

r* = x·(1+x)·(1+x+x²) = x + 2x² + 2x³ + x⁴ (=x + x² + x² + x³ + x³ + x⁴),

and

g* = x·(1+x)·(1+x+x²)·(1-x+x²)² = x + x³ + x⁴ + x⁵ + x⁶ + x⁸.

We get the unique second basic solution by reading the exponents of r* and g*. As in the direct solution, we see that the only alternative to ordinary dice is the pair with faces r* = (1, 2, 2, 3, 3, 4) and g* = (1, 3, 4, 5, 6, 8). By the way, note that the coefficients in all the polynomials that appear in these factorizations and products have an obvious symmetry. This is precisely the symmetry we used to simplify our first solution.