What can be said about four points in space with the property that every sphere or plane through the first two meets every sphere or plane through the second two?
Solution to MP35
During the month of October 2003 we had substantial email problems at Math Central which may account for the fact that we only received one solution. That one correct solution was from Patrick LoPresti (USA). He showed that
If A, B, C, and D are four distinct points for which every sphere or plane through A and B meets every sphere or plane through C and D, then these four points lie on a line or on a circle in such a way that the pairs A, B and C, D separate each other. Conversely, if A, B and C, D separate each other, then each sphere or plane through A and B meets (or coincides with) each sphere or plane through B and D.
We begin with four points A, B, C, D situated so that the spheres and planes through A and B meet all spheres and planes through C and D. LoPresti’s proof consists of three observations.
Observation 1. The lines AB and CD must intersect or
coincide.
Proof. Should, to the contrary, the minimum distance between
the lines be d > 0, then there would exist points P on AB and Q on CD for
which d = PQ > 0. Since d is the minimum distance, PQ must be perpendicular
to both AB and CD. Define ∏ to be the plane perpendicular to
PQ through its midpoint (and therefore parallel to both lines). Take
a point P’ on the perpendicular bisector of AB between the line
ABP and ∏, and take a point Q’ on the perpendicular bisector
of CD on the other side of ∏, between ∏ and the line CDQ.
Then the sphere through A, B, and P’ that has its center on the
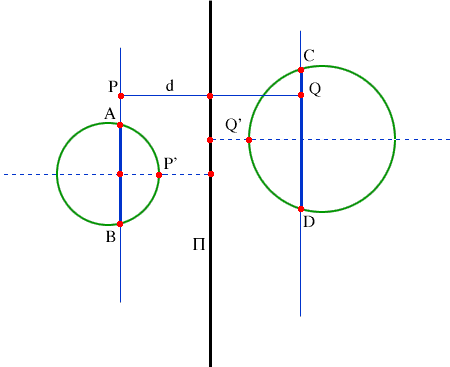
perpendicular bisector of AB will entirely lie on the opposite side of ∏ from the sphere through C, D, and Q’ that has its center on the other perpendicular bisector. In particular, these would be two nonintersecting spheres, one through A and B, the other through C and D, which contradicts the basic property of these points.
Remark. An immediate consequence of Observation 1 is that the given points lie in a plane, and our problem has been reduced to a problem in plane geometry. A complete treatment of this planar version can be found in Geometry Revisited by H.S.M. Coxeter and S.L. Greitzer (Mathematical Association of America, New Math Library No. 19 (1967), Theorem 5.11 on page 104. Their discussion is, in turn, based on a problem from the William Lowell Putnam Competition for 1965.
Observation 2. A, B, C, D lie on a line or a circle.
Proof. Suppose these points do not all lie on a line. Since AB
intersects CD, the perpendicular bisector of AB must intersect
the perpendicular bisector of CD. Let O be their intersection
point. If the sphere with center O through A and B were to have
a different radius from the concentric sphere through C and D,
we would have constructed
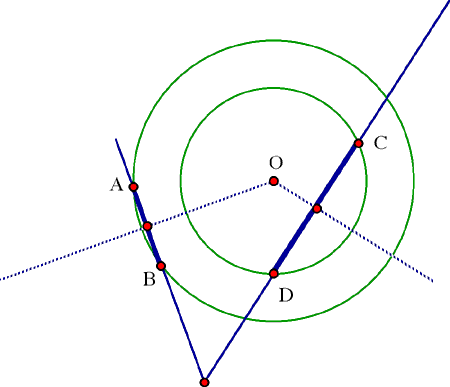
a sphere through A and B that fails to meet the sphere we constructed through B and D, contrary to the basic property of the four given points.
Observation 3. The pairs A, B and C, D
separate each other. (When the points are collinear this means
that one of A or B lies between
C and D, while the other lies on the line outside segment CD;
when concyclic, then one of the two arcs determined by C and D
contains
A while the other contains B.)
Proof. Should the points be collinear with A,B and C,D not separating
each other, as shown in the diagram, the sphere with AB as diameter
would be disjoint from the sphere
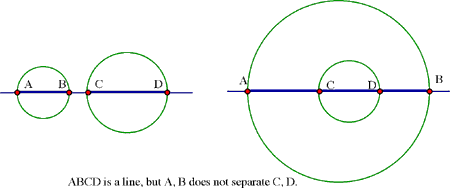
whose diameter is CD. Should the points be concyclic with A,B and C,D not separating each other, then the plane that is perpendicular to ABCD which contains the bisector of the angle formed by AB and CD would have A and B on one side, C and D on the other.
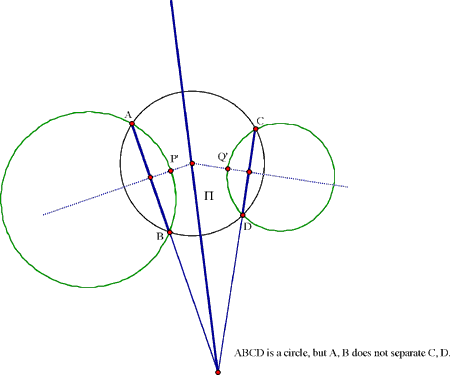
Thus, a construction along the lines of that in Observation 1 would produce a sphere through A and B that lies on one side of the dividing plane, with a sphere through C and D on the other side. Again, that would violate the basic property of the given points.
This completes the proof that the intersecting-sphere property forces the given pairs of points to separate one another. We turn now to the converse.
The converse. If A,B and C,D separate each other, then every
sphere or plane through A and B will meet every sphere or plane through
C and D.
Proof. Any sphere or plane through A and B that contains the
circle or line ABCD will meet any sphere or plane through C and D in the
points C and D, so there is nothing to prove. Let us therefore let S be
a sphere or plane through A and B that does not contain C or D. S meets
the circle or line ABCD in precisely the two points A and B.
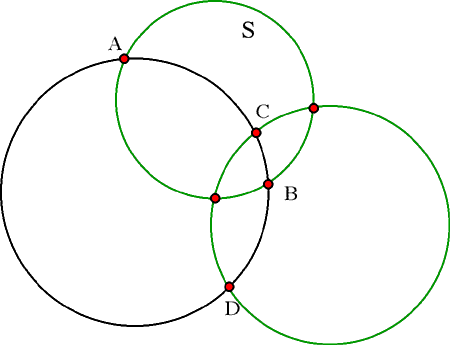
This implies that the portion of ABCD containing C is on one side of S while the portion containing D is on the other. Any sphere or plane through C and D therefore has points on either side of S, which means that it intersects S as claimed.