Solution to April 2005 Problem
The lengths of consecutive sides of a plane quadrangle are 6, 33, 47, and 34. What is the angle between the two diagonals?
(Although these side lengths might look as if they have been chosen at random, they weren't.)
We received correct solutions this month from
Mehdi Abdeh-Kolahchi (Halifax) |
Xavier Hecquet (France) |
|
Theerasak Asawanonwiwat (Thailand) |
Eric Hsiung (USA) |
|
Bernard Carpentier (France) |
Normand LaLiberté (Ontario) |
|
K.A. Chandrashekara (.com) |
Arne Loosveldt (.com) |
|
Pablo de la Viuda (Spain) |
Patrick LoPresti (USA) |
|
H.N. Gupta (Regina) |
Wolfgang Kais (Germany) |
Answer:
The angle between the two diagonals is 90º.
We all know that if you prescribe the side lengths of a triangle, you fix its shape. By contrast, the shape of our quadrangle ABCD is not fixed even though we have prescribed its sides to have lengths 6, 33, 47, and 34: if you build a quadrilateral out of four sticks of length p, q, r, s, with hinges at the vertices, you can deform it — or "smoosh it around", in LoPresti's words — as you can the quadrilateral in Figure 1. (You can move point C without changing the lengths p, q, r, s.) We chose the sides p, q, r, s in Figure 1
Figure 1
to satisfy p + s = q + r, making it obvious that the angle between AC and BD is not constant — you can see that it goes from positive to zero as A and C move toward the diagonal BD. It is therefore rather surprising that when AC is perpendicular to BD in one position, it will stay perpendicular in all positions (as in Figure 2 in which, here, A can be
Figure 2
moved, as can the side lengths of the auxiliary quadrangle). Indeed, in his solution Chandrashekara simply referred to Peaucellier's theorem:
The sum of the squares on the opposite sides of a quadrilateral are
equal if and only if the diagonals are perpendicular.
In our quadrilateral, p = 6, q = 33, r = 47, and s = 34, and so
p2 + r2 = 62 + 472 = 2245 = 332 + 342 = q2 + s2.
We shall discuss the theorem's history and significance at the end. First we present three different proofs, each restricted to our specific case. You can replace the four given numbers by p, q, r, s to obtain the general proof with each approach.
1. Proof by coordinates. (The method of Hecquet and Kais.)
We shall modify Hecquet's solution by choosing the origin to be at vertex B and placing D at some point (k, 0) on the x-axis. The point A will then be one of the two points where the circle centered at B of radius 33 meets the circle centered at D of radius 6. The coordinates (x, y) of A therefore must satisfy
x2 + y2 = 332 = 189 and (x - k)2 + y2 = 62 = 36.
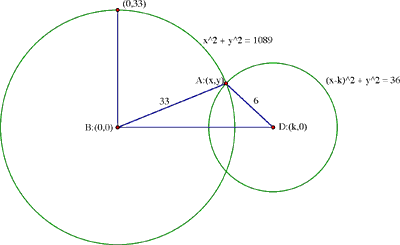
Figure 3
Subtract the second from the first to find that 2kx – k2 = 1053, so that the x-coordinate of A must satisfy
Similarly, the coordinates (x, y) of C satisfy
x2 + y2 = 472 = 2209 and (x - k)2 + y2 = 342 = 1156.
Subtract the second from the first, and we see that the x-coordinate of C must equal the x–coordinate of A. That is, both A and C lie on the vertical line x = (1053 + k2)/2k; in other words, AC is perpendicular to BD.
We received a second solution from Carpentier that provides the same argument in vector notation. He uses a symmetric notation, but we will place the origin at B so that we may write vectors BX simply as X. The length of X is X · X, which we write as X2. Then the equality of the sum of the squares of opposite sides of ABCD is equivalent to each of the following equations:
A2 + CD2 = C2 + AD2
A2 + D2 – 2C · D + C2 = C2 + A2 – 2A · D + D2
C · D – A · D = 0
(C – D) · D = 0
The last equation says that the vector from C to A is perpendicular to the vector from the origin (namely B) to D.
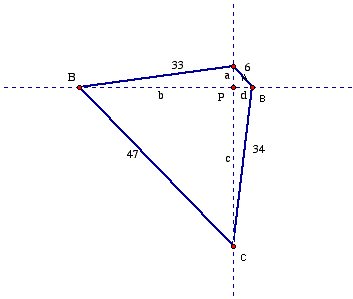
2. Proof using the cosine law (the method of Abdeh-Kolahchi, Asawanonwiwat, Carpentier, Chandrashekara, de la Viuda, LaLiberté, Loosveldt, and LoPresti).
We shall present a combination of the similar arguments of Abdeh-Kolahchi, de la Viuda, and LoPresti. Let the diagonals AC and BD intersect at P (labeled as in Figure 2). Denote the distances from P to A, B, C, and D by a, b, c, and d, respectively, and let q = <APB. Recall that cos q = –cos(180º – q). By the cosine law applied in turn to triangles APB, BPC, CPD, and DPA,
332 = a2 + b2 – 2ab cos q, 472 = b2 + c2 + 2bc cos q, 342 = c2 + d2 – 2cd cos q, 62 = d2 + a2 + 2da cos q. |
|
Subtracting the first and third equations from the sum of the second and fourth, we find that
472 + 62 –332 – 342 = 2(ab + bc + cd + da) cos q
We have seen already that the left-hand side is 2245 – 2245 = 0, If we can show that 2(ab + bc + cd + da) > 0, it would immediately follow that cos q = 0, so that q = 90º, as desired. Since ab + bc + cd + da = (a + c)(b + d) = AC·BD, and since all of a, b, c, d represent distances from P, were a + c to be zero, we would have (by definition) A = C = P; but A and C could not both lie on BD since 33 + 6 ≠ 47 + 34. Similarly, b + d ≠ 0, so their product is also nonzero, and the proof is complete.
3. Proof using the Pythagorean Theorem. (This is the method of Gupta, Hsiung, and of Carpentier's second proof.)
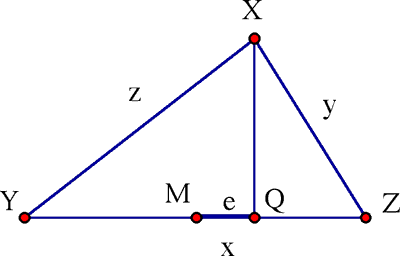
Figure 4
Lemma. In any triangle XYZ whose sides satisfy z ≥ y, the altitude from X meets the opposite side YZ at a point Q whose distance from the midpoint is
Proof. Pythagoras tells us that XQ2 = YX2 – YQ2 = ZX2 – ZQ2, so that
Expanding and simplifying, we get z2 – y2 = 2xe, so that e = ( z2 – y2)/2x as claimed.
We apply the lemma to our triangles ABD and CBD. In Figure 2 above we have DABD on top with z = 33, y = 6, and X = BD, so that
Below, we have DCBD with z = 47, y = 34, and x = BD, so that
has the same value. Thus the perpendiculars to BD from A and from C meet BD at the same distance from its midpoint. Since there can be only one line perpendicular to BD at that point, that line must be the diagonal AC; we conclude that AC is perpendicular to BD.
Historical background.
Charles-Nicolas Peaucellier (1832-1913) was a captain in the French army's engineer corps in 1864 when he invented the Peaucellier cell ["... outlined in general terms and in question form in les Nouvelles Annales mathématiques, page 414; his detailed exposition appeared in the same journal in 1873, page 71."]. This Peaucellier cell is a linkage that draws the inverse of any locus, thus providing for the first time an exact solution to the mechanical problem of converting circular into rectilinear motion: in Figure 5, as D traces out a circle passing through B, D' moves along a line perpendicular to the diameter through B of that circle. The device is formed by two rods of length r and two of length s, hinged at the corners B and C of a kite-shaped quadrangle ADCD', with longer rods of length p and q connecting the opposite corners A and C to a fixed pivot at B. As a
figure 5
figure 5
consequence of his theorem, the product BD·BD' will be constant. The proof of this claim is similar to the argument we used in proof 3 as follows (see Figure 6): p2 – b2 = a2 = s2 – d2, and so
p2 – s2 = b2 – d2 = (b – d)·(b + d) = BD·BD'.
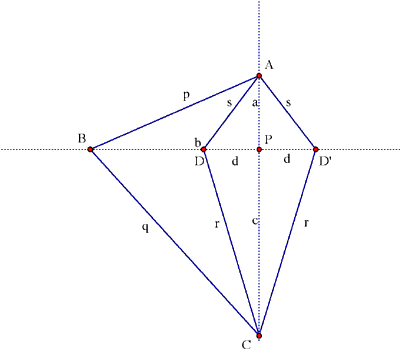
Figure 6
Under the assumption that p2 – s2 = q2 – r2 (which we
have seen is equivalent to AC perpendicular to BD when the longer sides
p and q come from the same vertex) the product BD·BD' is constant
when the lengths p, q, r, and s are fixed. By definition this
means that D' will be the inverse of the point D in a circle whose
center is B and radius is 
. Thus,
as a pointer at D is traced over the curves of a given figure, a pencil
placed at D' draws the inverse figure; in particular, if a seventh
rod and another pivot are introduced so as to keep D on a circle that
passes through B, the locus of D' will be a straight line. The
whole story is told in geometry books that discuss inversion (such
as H.S.M. Coxeter, Introduction to Geometry, Chapter 6), or
books that deal with the geometry of complex numbers (under the names
linear fractional or Möbius transformation). See also the
web pages
http://mathworld.wolfram.com/Inversion.html and http://www.cut-the-knot.org/pythagoras/invert.shtml.
There are many other web pages that discuss the Peaucellier cell; just ask Google to find them for you. We found Peaucellier's full name and life span on the page http://sunsite.utk.edu/math_archives/.http/hypermail/historia/feb99/0014.html. (We have not confirmed that information.) We took the information about Peaucellier's theorem from Exercices de géométrie, 4th ed (1907), by F. G.-M, pages 505, 506, and 513.