Solution to February 2005 Problem

Double-zapping

            This month we show how television can be used for educational purposes. Suppose that you have two televisions side by side, Television A and Television B, that are activated by separate remote controls. We call double-zapping the act of simultaneously pressing the channel up or channel down button of A's remote and the channel up or channel down button of B's remote. For instance, from (Channel 8, Channel 6) you can double-zap to any one of (Channel 7, Channel 5), (Channel 7, Channel 7), (Channel 9, Channel 5) or (Channel 9, Channel 7).

            For this month's problem you actually have three televisions side by side, each activated by its own (distinct) remote and connected to different cable companies:

Television A is connected to cable company Alpha which has 70 channels A1 to A70,
television B is connected to cable company Beta which has 60 channels B1 to B60, and
television C is connected to cable company Gamma which has 94 channels C1 to C94.

However, you find that there are very few different networks, each of which is duplicated over and over; moreover the networks are exactly the same on all three cable company; in particular, channel A1 is the same as channel B1 and channel C1, and channel A70 is the same as channel B60 and C94.  Eventually you find out that it is possible to start from (A1, B1) and double-zap all the way to (A70, B60) in such a way that the program displayed on television A is always the same as the program displayed on television B. Similarly, it is possible to start from (B1, C1) and double-zap all the way to (B60, C94) in such a way that the program displayed on television B is always the same as the program displayed on television C.

The February problem: In these circumstances is it necessarily possible to double-zap from (A1, C1) to (A70, C94) in such a way that the program displayed on television A is always the same as the program displayed on television C.

WARNING: Do not attempt to push the channel down button when a television is on channel 1; similarly, do not attempt to push the channel up button when a television is on the top channel. This would cause the corresponding television to explode, and might void your insurance policy.

Solution.
Yes, it is always possible to double-zap from (A1, C1) to (A70, C94) in such a way that the program displayed on television A is always the same as the program displayed on television C. In fact, it is possible to triple-zap from (A1,B1,C1) to (A70,B60,C94) -- a feat well worth trying by those who have enough dexterity in their right foot.

We received a partial solution from Xavier Hecquet (France), where he indicated that the problem is easier to solve when all the channels on B are different. In this case, we can go from (A1,B1) to (A70,B60) by always pressing the channel up button on A's remote. Indeed, if we press A's channel up button to go from (Ai,Bj) to (Ai+1,Bj') and then A's channel down button to go to (Ai,Bj''), then j'' = j (since all of B's channels are different), so the last two steps cancel each other out. We will first solve the case where all the channels on B are different.

Solution 1: Different channels on B carry different programs.

We will form a graph G whose vertices are all the couples (Ai,Ck) which correspond to a common Bj, and where two couples (Ai,Ck) and (Ai',Ck') are connected if we can double-zap from one to the other.

For instance the table above corresponds to a smaller example where B has three different channels, and A, C have nine channels each. The graph G we consider is the following:

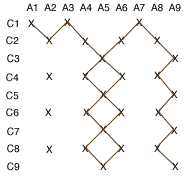
Among other things, the graph contains some isolated vertices like (A2,C6), and the long winding path (A1,C1), (A2,C2), (A3,C1), (A4,C2), (A5,C3), (A6,C2), (A7,C1), (A8,C2), (A9,C3), (A8,C4), (A9,C5), (A8,C6), (A9,C7), (A8,C8), (A9,C9). We will show that such a path from (A1,C1) to (Alast,Clast) necessarily exists, using the following local property of the graph:

Lemma 1: If A has m channels and C has n channels, then (A1,C1) and (Am,Cn) have exactly one neighbour each, and all the other vertices of G have an even number of neighbours.

Proof. Suppose that the couple (Ai,Ck) corresponds to Bj, where 1 < i < m and 1 < k < n.

Since we can double-zap from (A1,B1) to (Am,Bt) (where t is the number of channels on B), The channels Ai-1 and Ai+1 each correspond to one of Bj-1, Bj+1. Similarily, since we can double-zap from (B1,C1) to (Bt,Cn), the channels Ck-1 and Ck+1 each correspond to one of Bj-1, Bj+1. For instance, Ai-1 and Ck-1 could correspond to Bj-1, and Ai+1, Ck+1 could correspond to Bj+1, and then (Ai,Ck) has the two neighbours (Ai+1,Ck+1) and (Ai-1,Ck-1). There are in all sixteen similar cases, which we list in the table below.

Exceptions occur on the boundaries, that is, when i = 1 or m, or k = 1 or n. When i = 1 and 1 < k < n, we have A1 = B1 = Ck hence A2 = B2 = Ck-1 = Ck+1, so that (A1,Ck) has the two neighbours (A2,Ck-1) and (A2,Ck+1). Similarly, all couples of type (Am,Ck), 1 < k < n, (Ai,C1) or (Ai,Cn), 1 < i < m have exactly two neighbours. The two couples (A1,C1) and (Am,Cn) each have one neighbour, (A2,C2) and (Am-1,Cn-1) respectively, and none of the couples (A1,Cn) and (An,C1) belong to the graph since A1 = B1 which is different from Bt = Cn, and An = Bt which is different from C1 = B1. This completes the proof of the lemma.

The number of neighbours of a vertex of a graph is called the "degree" of that vertex. Lemma 1 states that every vertex in our graph has even degree, except (A1,C1) and (Am,Cn), which have degree 1. One of the basic results in graph theory is the following.

Lemma 2: In any graph, the number of vertices of odd degree is even.

Short proof: If we sum up all the degrees of the vertices in a graph, we get twice the number of edges, because we counted every edge twice. Thus we can divide this sum by 2 to get the number of edges, which is a whole number. Hence the number of odd degrees was even. That's all. A simple observation is the key to Euler's solution to the Königsberg bridge problem.

Note that it is consistent with what we know of G, which has exactly two neighbours of odd degree, namely (A1,C1) and (Am,Cn). Is there anything more to say? Yes! What we need to do is apply Lemma 2 to a smaller graph H consisting of the vertices of G which are reachable from (A1,C1) by a sequence of double-zaps. That is, (A1,C1) is in H, and whenever a vertex (Ai,Ck) of G is in H, then all of its neighbours are also in H. Thus the degree of a vertex of H is the same as its degree in G. Since H contains the vertex (A1,C1) of degree 1, it must contain a second vertex of odd degree. However the only candidate is (Am,Cn), which means that (Am,Cn) must also belong to H. Therefore it is possible to move from (A1,C1) to (Am,Cn) by a sequence of double-zaps.

Unfortunately, this beautiful argument does not work when the channels on B are repeated. For instance, in our example above, if we replace all 3s by 1s, then we need to add many vertices to G, including (A1,C9) which will be of degree 1. We will see below how to adapt the proof to the general case.

Solution 2: The general case.

Let television A, B and C have respectively m, t and n channels, labeled A1 through Am, B1 through Bt and C1 through Cn, If it is possible to double-zap from (A1,B1) to (Am,Bt) in such a way that the program displayed on A is always the same as the program on B, and from (B1,C1) to (Bt,Cn) in such a way that the program displayed on B is always the same as the program on C, then it is possible to double-zap from (A1, C1) to (Am, Cn) in such a way that the program displayed on A is always the same as the program displayed on C.

Proof: For simplicity we will call a double-zap "coherent" when it jumps from identical channels to identical channels. Let P be a path corresponding to a shortest sequence of coherent double-zaps from (A1,B1) to (Am,Bt). That is, P = { (A1,B1), (A2,B2), (Ai3,Bi3), (Ai4,Bi4), ..., (Am-1,Bt-1), (Am,Bt)}. The same channel Ai can be the first coordinate of many couples in P, and the same channel Bj can be the second coordinate of many couples in P. However a couple (Ai,Bj) cannot occur twice in P, otherwise P could be shortened. Similarly, let Q = {(B1,C1), (B2,C2), (Bj3,Cj3), ..., (Bt-1,Cn-1), (Bt,Cn)} be a path corresponding to a shortest sequence of coherent double-zaps from (B1,C1) to (Bt,Cn). We form the graph G whose vertices are the triples (Ai,Bj,Ck) such that (Ai,Bj) is in P and (Bj,Ck) is in Q, where (Ai,Bj,Ck) is joined to (Ai',Bj',Ck') when (Ai,Bj) is a neighbour of (Ai',Bj') in P and (Bj,Ck) is a neighbour of (Bj',Ck') in Q.

We will again show that (A1,B1,C1) and (Am,Bt,Cn) are the only vertices of odd degree in G, And just as in solution 1, this means that there exists a sequence of coherent triple-zaps that starts at (A1,B1,C1) and ends at (Am,Bt,Cn).

Lemma 3: All the vertices in G have even degree, except (A1,B1,C1) and (Am,Bt,Cn) which have degree 1.

Proof of Lemma 3: Let (Ai,Bj,Ck) be a vertex of G. Usually, (Ai,Bj) will have two neighbours (Ai',Bj'), (Ai'',Bj'') in P, and (Bj,Ck) will have two neighbours (Bj''',Ck'), (Bj'''',Ck'') in Q. This means that each of i', i'' is either i-1 or i+1, each of j', j'', j''', j'''' is either j-1 or j+1, and each of k', k'' is either k-1 or k+1. The possible neighbours of (Ai,Bj,Ck) are the four triples (Ai',Bj',Ck'), (Ai',Bj',Ck''), (Ai'',Bj'',Ck') and (Ai'',Bj'',Ck''). (Ai',Bj',Ck') is a neighbour of (Ai,Bj,Ck) if and only if j' = j''', (Ai',Bj',Ck'') is a neighbour of (Ai,Bj,Ck) if and only if j' = j'''', (Ai'',Bj'',Ck') is a neighbour of (Ai,Bj,Ck) if and only if j'' = j''' and (Ai'',Bj'',Ck'') is a neighbour of (Ai,Bj,Ck) if and only if j'' = j''''. Since all of j', j'', j''' and j'''' are either j-1 or j+1, the number of equalities between j', j'' on one side and j''', j'''' on the other is even, hence the degree of (Ai,Bj,Ck) is even. The boundary cases of type (A1,B1,Ck), (Am,Bt,Ck), (Ai, B1,C1) and (Ai,Bt,Cn) are easily seen to be of degree 2, except for (A1,B1,C1) and (Am,Bt,Cn) which are of degree 1. This concludes the proof of the lemma and our solution.

Comme dans la première solution, nous démontrerons que (A1,B1,C1) et (An,Bt,Cm) sont les seuls sommets de degré impair dans G, ce qui impliqu'il existe une série de triple-zaps cohérents de (A1,B1,C1) à (Am,Bt,Cm). En laissant tomber la télécommande de B, on en tire une série de triple-zaps cohérents de (A1,C1) à (Am,Cn).

Lemme 3: Tous les sommets de G ont degré pair, sauf (A1,B1,C1) et (Am,Bt,Cn) qui ont degré 1.

Démonstration du Lemme 3: Soit (Ai,Bj,Ck), un sommet de G. En général, (Ai,Bj) a deux voisins (Ai',Bj'), (Ai'',Bj'') dans P, et (Bj,Ck) a deux voisins (Bj''',Ck'), (Bj'''',Ck'') dans Q. Chacun de i' et i'' est alors i-1 ou i+1, et de même chacun de j', j'', j''', j'''' est j-1 ou j+1 et chacun de k', k'' est k-1 ou k+1. En particulier j', j'', j''' et j'''' prennent en tout au plus deux valeurs, donc il y a égalité entre certains de ces termes. Les voisins de (Ai,Bj,Ck) correspondent aux égalités entre d'une part j' ou j'' et d'autre part j''' ou j''''; par exemple, si j'' = j''', alors (Ai'',Bj'',Ck') est voisin de (Ai,Bj,Ck). Or puisque j', j'', j''' et j'''' prennent au plus deux valeurs, il y a un nombre pair de ces égalités, donc (Ai,Bj,Ck) a un nombre pair de voisins. On voit facilement que les sommets de frontière de type (A1,B1,Ck), (Am,Bt,Ck), (Ai, B1,C1) et (Ai,Bt,Cn) sont tous de degré 2, sauf (A1,B1,C1) et (Am,Bt,Cn) qui sont de degré 1. Le lemme est ainsi démontré, ce qui complète la solution.