Solution to March 2005 Problem
If the real numbers x and y satisfy
![]()
find their sum x + y.
We thank Andy Liu of the University of Alberta for this month's problem.
We received correct solutions from
Anurag Agarwal (Buffalo, NY) |
Normand LaLiberté (Ontario) |
|
Said Amghibech (Quebec) |
Marc Lichtenberg (France) |
|
Ricardo Barroso (Spain) |
Patrick LoPresti (USA) |
|
Pierre Bornsztein (France) |
M. Loyer (France) |
|
Seymur Cahangirov (Azerbaijan) |
Hassan Moutaharir (Quebec) |
|
Bernard Carpentier (France) |
Dat Phan (Regina) | |
| Pablo de la Viuda (Spain) | Anonymous | |
| Xavier Hecquet (France) | Tran Tranh Phuong (.com) | |
| Wolfgang Kais (Germany) | Richard Wood (Dartmouth NS) |
The answer is x + y = 0. There were many interesting approaches to the solution, and Hecquet single-handedly provided a version of each. We shall use his rubrics together with a combination of nice ideas from each contributor. Most of the solutions make use of an easily verified fact:
![]()
Note that when the product of two expressions is 1, neither can be zero.
1. A la hussarde (The method of Agarwal, de la Viuda, Kais, LaLiberté, Phan, and Wood). The idea here is to get rid of the radicals by squaring, but even a hussar would simplify things a bit before squaring. Among the various possibilities for simplification, we can use our basic fact to rewrite the given equation ![]() as
as
![]()
Square both sides
![]()
then subtract 1 from both sides to get,
![]()
Since the terms in parentheses are equal and nonzero, we can cancel them and divide by 2 to get y = –x, so that x + y = 0, as claimed. Of course, after we square the sides of an equation we must check that no new solutions have been introduced: one checks easily that y = –x satisfies the given equation.
2. Un peu plus fûté. (The method of Amghibech, Barroso, and Moutaharir.)
This time let's use our basic fact twice (once with x and once with y):
![]()
Add these two equalities to find x + y + R = –(x + y) + R, where R is the sum of two radicals; thus, 2(x + y) = 0, which again reduces to x + y = 0.
3. A la Euler. (The method of Cahangirov, Lo Presti, Loyer, Anonymous, and Tran.)
Let ![]() Then
Then ![]() so that k2 -2x + x2 = x2 - 1 from which
so that k2 -2x + x2 = x2 - 1 from which
![]()
The given equation implies that ![]() which (by using the same steps as before) leads to
which (by using the same steps as before) leads to
![]()
Adding these two expressions, we find that x + y = 0.
Comment. Those who are familiar with hyperbolic functions will recognize what is going on here. The hyperbolic functions are related to the hyperbola x2 – y2 = 1 in a manner analogous to the relation of the trigonometric functions to the circle x2 + y2 = 1. (Actually, the hyperbolic functions were not introduced by Euler, but by his contemporary Vicenzo Riccati (1707-1775), so maybe we should have entitled method 3, "A la Riccati.") The hyperbolic sine
![]()
(usually pronounced "sinch") and the hyperbolic cosine
![]()
satisfy the basic relation
cosh2 a - sinh2 a = 1.
Other easily verified identities that we use here are cosh a + sinh a = ea and sinh(–a) = –sinh a. Note that cosh a is strictly positive (that is, ![]() ); it takes every value greater than 1 exactly twice. On the other hand, sinh a is strictly increasing, taking all real values from –∞ to ∞ once and only once; in particular, there is a u and a v for which sinh u = x and sinh v = y. If it is not yet obvious, here is their relationship to the previous argument: define u = ln k; that is, eu = k. The above equation for x then becomes
); it takes every value greater than 1 exactly twice. On the other hand, sinh a is strictly increasing, taking all real values from –∞ to ∞ once and only once; in particular, there is a u and a v for which sinh u = x and sinh v = y. If it is not yet obvious, here is their relationship to the previous argument: define u = ln k; that is, eu = k. The above equation for x then becomes
![]()
So, here is the argument once again in the revised notation. The given equations become
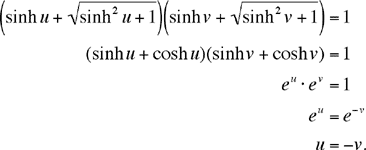
This last equation implies that sinh u = sinh(–v) = –sinh v, which says that x = –y, so that x + y = 0.
4. Euler bis. (The method of Carpentier and Lichtenberg.)
Here we use the inverse hyperbolic functions: x = sinh u if and only if u = sinh-1x. It is easily verified that
![]()
This observation leads to the equivalent equations
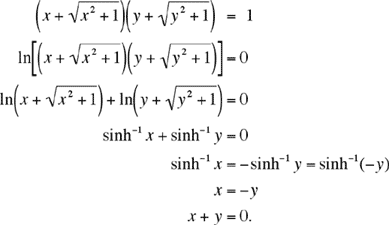
5. Appel à l'âne à Lise. (Bornsztein's method.)
The argument above in (4) is easily seen to apply in a more general setting. We start by setting ![]() .
We note that
.
We note that ![]() that is,
that is,
f(x) > 0.
Furthermore,
x < 0 if and only if f(x) < 1,
since the latter inequality is equivalent to ![]() which (by squaring the equal positive numbers) says simply that 0 < -2x. On the other hand, from the definition of f(x),
which (by squaring the equal positive numbers) says simply that 0 < -2x. On the other hand, from the definition of f(x),
x > 0 if and only if f(x) > 1.
Consequently, if f(x)f(y) = 1 we can assume without loss of generality that x ≤ 0 ≤ y. Our basic fact says that f(x) satisfies 1/f(x) = f(–x), so our given equation is
f(y) = f(-x).
Because f(x) is the sum of two functions that are strictly increasing as x runs from 0 to infinity, f(x) itself is strictly increasing. Since y ≥ 0 and –x > 0, we deduce that y = –x and, therefore, x + y = 0.
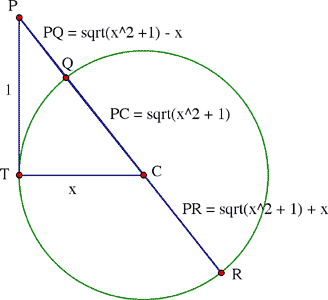
6. A la Euclid. This approach was unique to Hecquet. He presented only the start of a pictorial argument. We modified it a bit and (in the words of people who don't quite know how to finish the argument) we leave the details to the reader. Our picture is based on two Euclidean theorems:
- If a secant from an external point P meets a circle at the points Q and R, and one tangent from P touches that circle at T, then PQ x PR = PT2.
and
- The radius from the center C to a point T on the circle is perpendicular to the tangent at T.
The accompanying figure shows the right triangle PTC with legs x and 1 and hypotenuse ![]() so that
PQ x PR =
so that
PQ x PR = ![]()