Solution to September 2004 Problem
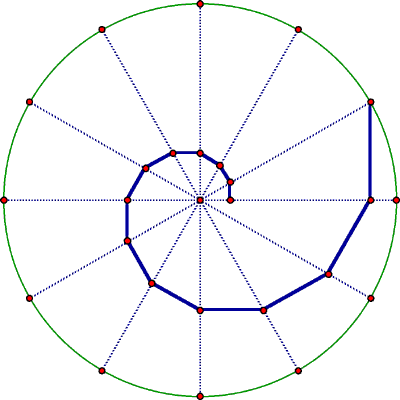
The unit circle is divided into twelve equal parts, and the twelve dividing points are joined to the circle's centre, producing twelve rays. Starting from one of the dividing points a segment is drawn perpendicular to the next ray in the clockwise sense; from the foot of this perpendicular another perpendicular segment is drawn to the next ray, and so on. What is the limit of the sum of the lengths of these segments?
Solution to MP43
We received correct solutions from
| Alex Akulov (Regina) | Wolfgang Kais (Germany) |
| Said Amghibech (Quebec) | Normand LaLiberté (Ontario) |
| Endre Balogh (Hungary) | Patrick LoPresti (USA) |
| Ricardo Barroso Campos (Spain) | Marian Marinescu(France) |
| Pierre Bornsztein (France) | Juan Mir Pieras (Spain) |
| Bernard Carpentier | Leigh Norris (USA) |
| Bruno Demarest (France(?)) | Fernando Szechtman(Regina) |
| Xavier Hecquet (France) | AWD ‘Silversprite’ |
| Pablo de la Viuda (Spain) |
Welcome back to our old friends, and welcome to all the newcomers. Thank you for your interesting solutions.
Everybody summed a series to determine that the length of the path is
.
After presenting the common solution, we’ll look at two geometric solutions from Xavier Hecquet, and various generalizations from Kais, Mir, and Szechtmen.
The series solution.
Let O be the centre, let P0 be the initial point on the unit circle, and let P1, P2, ..., be the feet of the successive perpendiculars. The resulting triangles OPnPn+1 are right triangles with angles of 30o at O and 60o at Pn:
The hypotenuse rn+1 = OPn+1 of the next triangle is cos (30o) times the hypotenuse rn of this triangle. Since cos (30o) = √3/2, we have
The polygonal path whose length we are computing is composed of the sides PnPn+1 of successive triangles; these have length rnsin(30o) = rn/2. Consequently, in the following triangle the contribution is
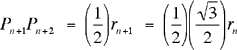
The sum of the first n+1 segments is therefore
P0P1 + P1P2 + P2P3 + ... + PnPn+1 =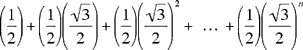 
which we recognize as a geometric progression with ratio √3/2; the sum is
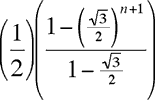
Since √3/2 < 1, (√3/2)n+1 goes to 0 as n goes to infinity, and it follows that the limit of the sum must be
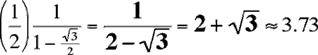
as claimed.
By looking at the appropriate diagram and using some basic trigonometry, you can determine the length of the path without the infinite sum formula. In fact, Hecquet sent us two pictures that solve our problem at a glance.
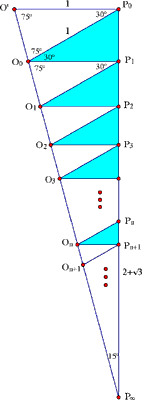
Picture 1.
Let’s unwind the path by sliding each triangle OPnPn+1 to a position OnP´nP´n+1 so that its right side P´nP´n+1 lies along the extension of side P0P1. These are the blue 30-60 right triangles in the figure. (Let’s drop the primes for simpler notation.) Since the
bottom side (OnPn+1) of each
triangle equals the hypotenuse (On+1Pn+1) of the next, each white
triangle OnPn+1On+1 is isosceles; they are all similar with an
angle of 30º at Pn+1 and angles of
75º at On and On+1. This forces the O’s
to lie along a line. In the limit, the line of O’s
and the line of P’s meet in the point labeled P
. The
length of the right side, namely P0P,
is the length of our polygonal path which has been straightened
out. By
completing the figure with a horizontal line O´P0 of length
1 at the top, we get a large right triangle with angel 75º at
O´ and 150 at
P (and right angle at P0). The desired length is therefore
P0P =
1/cot(150).
To see that this is the same answer as obtained in the series solution, use the half-angle formula:
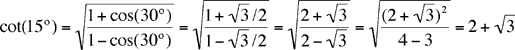
as expected.
Picture 2.
We again will line up the triangles of the sequence, but this time we flip every second triangle over, exchanging O with P2k+1. For example, we flip the second triangle P1OP2 so that O changes places with P1, and the side P1P2 lands on the left side
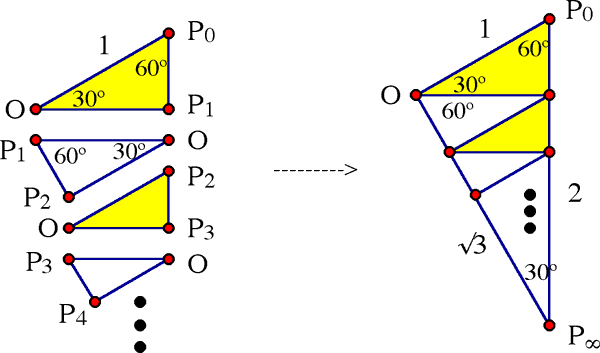
of the figure. You should check that half the segments
along our path (whose length we are to determine), namely P0P1,
P2P3, …, P2kP2k+1, …,
line up along the right side, while the others, P1P2,
P3P4, …, P2k+1P2k+2, …,
line up along the left. (The angles can be seen to insure
that these segments to lie along straight lines.) The resulting
figure P0OP is
a 30-60 right triangle whose top leg has length 1. The
left side OP therefore
has length cot(30º)
= √3, and its hypotenuse P0P has
length csc(30º)
= 2. The length of our path is the sum of these two numbers,
2 + √3.
Generalizations.
All
our arguments are easily modified if instead of starting with
the circle divided into twelve equal parts, we were to divide
it into n equal parts. More generally, we could set the
equal angles PnOPn+1 = φ.
The length of the path is then
.
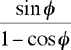We can also replace our perpendiculars by segments dropped to the next line at an arbitrary angle α < 90º. More precisely,
Points Q0, Q1, Q2, … are evenly spaced clockwise about the unit circle and joined to the centre O. We define a polygonal path P0P1P2… as follows: Let P0 = Q0, and define P1 to be the point on OQ1 for which angle P0P1Q1 = α. Continue so that Pn+1 is the point for which angle PnPn+1Qn+1 = α. Find the limiting length of the polygonal path as n approaches
The
pictorial proofs give a solution that is both surprisingly simple
and surprising! In each of the above pictures we simply
replace the 30º angles (at the points corresponding to O)
by φ, and the 60º angles (at
the points corresponding to Pn) by a – φ,
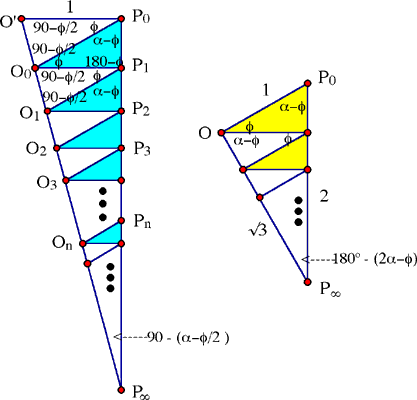
as in the figures below. In the diagram
on the left, the big triangle P0O´P has
angles α at P0 and 90º – φ/2
at O´; thus, the angle at P must
be 180º – α – 90º + φ/2 = 90º – (α – φ/2). Since
we want the length of P0P, we apply the sine
law to this triangle (which says that the quotient of a side
divided by the sine of the opposite angle is the same for all
three sides). That
is,
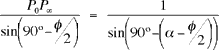or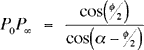 
Some trig identities are needed to see that this agrees with the expected answer when α = 90º as in the original problem:
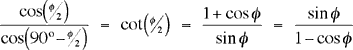
In the second figure, again P0OP is
a triangle, now with angles α – φ at P0,a at O’,
and (therefore) 180º – (2α – φ) at P. By
the sine law — and using sin(180º – (2α – φ)) = sin(2α – φ) — we see that
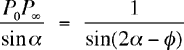and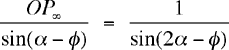 
Hence, the length of the path is P0P +
OP = 
.
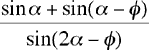These two approaches had better give us the same answer. That means, of course, that
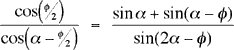
This is a trigonometric identity that you’re not likely to find in your textbooks.
Comment. Note that if f (the angle between successive radiating lines at O) is allowed to shrink to zero, the polygonal spiral tends toward the equiangular spiral (or logarithmic spiral) whose equation in polar coordinates is r = e(cota)θ. The curve intersects each radiating line (infinitely often) at the constant angle α. You can learn more about
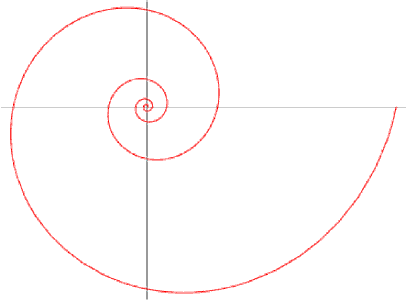
the curve on the Mathworld web page
(from which we took the picture) and in A Book of Curves by E.H. Lockwood (Cambridge University Press, 1971, Chapter 9, pages 98-109). Lockwood suggests a way to draw the curve: first construct the points Pn of a polygonal spiral using a small angle φ (such as φ = 10º), then connect the points so found by a freehand curve. Also, he discusses the “paradox” that an unending curve should have a finite length, pointing out that, “it depends on the precise meaning which we attach to the word end. Although there is no point of the curve itself which can be described as the end-point, nevertheless there is a point, namely the pole O, which the curve approaches and beyond which it does not go.” He goes on to produce a figure that is the infinite version of Hecquet’s first figure.
Another generalization.
Szechtman considers what happens if you divide the circle into n equal parts and sum only the first n segments along the resulting path. Here we must use radian measure for our angles, so we change the notation for the angle between successive radiating lines from f to x = 2π/n. We proceed as in the original problem, dropping perpendiculars from each point to the next line. As before, we find that the sum of the first n segments is
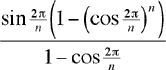
Now let’s let n go to infinity. The angle x = 2π/n goes to zero and the single turn of the spiral approaches the unit circle. This means that if we define
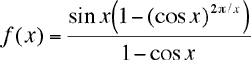
then the limit of f(x) as x tends to 0 from the right had better be 2π. For those readers who know about either l’Hôpital’s rule or Taylor series, it is a pleasant exercise to show that 2π is indeed the correct limit.