is a 30-60 right triangle with sides 1, 1/2, and √3/2. We may as well take D above the xy-plane, so that
D = (1, 1/2, √3/2).
Similar reasoning (interchanging the roles of x and y) gives us two possibilities for E:
E1 = (1/2, 1,
√3/2) or E2 = (1/2, 1,
-√3/2).
In the first case the distance from D to E is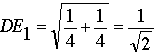 
; in the second, 
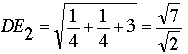. In either case, the distance from D to E is not 1.
Proof 2. Robinson showed somewhat more with his argument: An equilateral pentagon ABCDE in 3-dimensional space with unit sides and right angles at A, B, C, and D must have an angle at E of either 60° or cos-1(-5/√14) (which is about 111°); in particular, ∠E cannot be 90°. We will modify his notation to fit with the previous paragraph. Thus the coordinates for E are still (1/2, 1, √3/2) but since there is an unknown angle at E, we no longer have the length of DA to work with; we know only that D is in the plane x = 1, and that DC = 1, whence D = (1, cos δ, sin δ) for some angle δ. To find cos δ we use ED = 1 to get
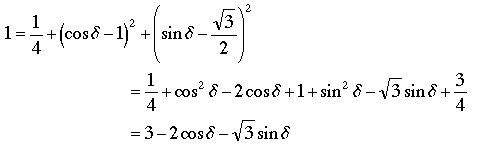
which simplifies to
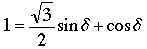. (1)
We wish to solve (1) for cos δ; Let c = cos δ and replace sin δ by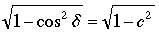 
;
then (1) becomes
,
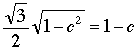so that (by squaring)
.
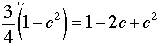We solve this quadratic equation for c and find that
c = cos δ = 1 or 1/7. (2)
Finally, the cosine of the angle we seek is then the scalar product of unit vectors,
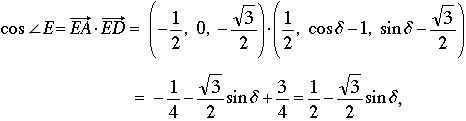
which, from (1), equals cos δ– ½; Equation (2) now tells us that the cos ∠E = 1– ½ = ½, or cos ∠E =1/7 - 1/2 = -5/14, as claimed.
Further comments. LoPresti suggested we call for a four-dimensional plumber — a pentagon with unit sides and five right angles is easily constructed in four dimensions! One way to see this is to put it in the 4-dimensional subspace u + v + x + y + z = √2 of 5-dimensional space. One then easily checks that the pentagon whose vertices are
(1/√2, 1/√2, 0, 0, 0), (0, 1/√2, 1/√2, 0, 0), (0, 0, 1/√2, 1/√2, 0),
(0, 0, 0, 1/√2, 1/√2), (1/√2, 0, 0, 0, 1/√2),
has edges of length 1 and diagonals of length √2 (which implies that the angles between consecutive edges are 90°). LoPresti says nothing about what 4-dimensional plumbers charge these days; one can only imagine that the cost would be out of this world.
Haider's solution was completely different. She considered the five vectors that join each vertex of the pentagon to the next, and determined that any four of them must be linearly independent; consequently the smallest space in which the pentagon could exist would necessarily have four dimensions.
Hexagons, heptagons, and other n-gons with n > 5.
People say that seeing is believing:
Mathematicians, however, say that one shouldn't believe everything one sees:
Penrose Triangle in a park in Gotschuchen, Austria
Picture reproduced from the Wikipedia files.
Because the angles of a triangle sum to 180°, no triangle can have more than one right angle. The illusion of a triangle with three right angles was, according to Wikipedia, first devised in 1934 by the Swedish artist Oscar Reutersvärd; it was independently discovered and popularized by the mathematician Roger Penrose and his father Lionel Penrose, the distinguished British psychiatrist and geneticist.
It is easy to prove the existence of right-angled hexagons without resorting to coordinates: use the edges surrounding the region formed by two adjacent faces of a cube (as in the picture using pipes above, and in the diagram below on the left). Lim and Golfman both described a second example using the edges of a cube: take edges along a path for which every two consecutive sides, but no three, belong to a face of the cube (as below on the right).
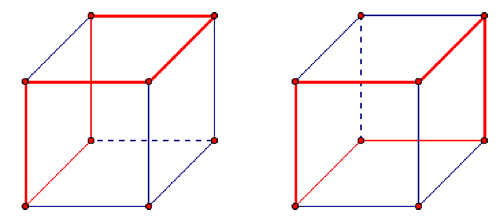
Here are the paths shown in the figures (starting with (0, 0, 0) in the back at the lower left):
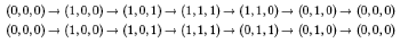
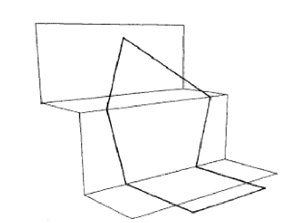
For the heptagon, it might help to imagine the figure laid out on a flight of stairs. The portion on the bottom stair consists of three sides of a square. Consider the vertical
central portion that consists of two sides of an isosceles trapezoid ABCD with AB = BC = CD = 1, and AD || BC with AD = √2. As shown in the diagram below, one can think of the isosceles right triangle ADP as a flap that rotates about a hinge AD. When the flap
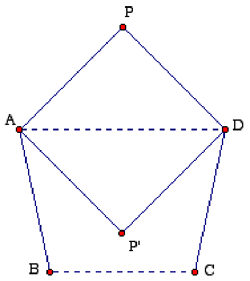
is "open" (with P outside the trapezoid, but in the same vertical plane), ∠BAP >∠P'AP = 90°; with the flap "closed" (in the position AP'D), ∠BAP' < ∠BAD < 90°. Somewhere between these two positions ∠BAP = ∠CDP = 90°. There will also be a symmetric position of the flap on the other side of the vertical plane where the angle between adjacent sides is 90°. Although half the correspondents used a similar dynamic argument to prove the existence of a right-angled heptagon, everybody supplied coordinates for good measure. Here are the coordinates that go up the stairs on the right (with the positive x, y, and z axes pointing to the right, in, and up, respectively):
.
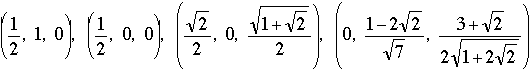The three vertices on the left in the stair figure have negative x-coordinates, but the same values for y and z. One checks easily that the distance between consecutive vertices is 1, and the angle between consecutive sides is 90°.
Final comments.
As several correspondents pointed out, there exist equilateral right-angled n-gons for n = 4, and for all n ≥ 6 — only 3 and 5 fail to exist. From a k-gon whose end consists of three sides of a square (such as, for example, the left 6-gon in the figure above and our 7-gon on the above stair figure), we construct a (k+2)-gon by replacing
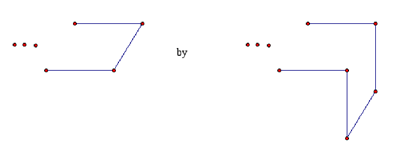
k-gon (k+2)-gon
The figure showing the heptagon on the stairs came from the solution to Problem 1110 (proposed by Gerald Wildenberg) in Mathematics Magazine, 55 (1982) 47-48, which was the source of our problem this month.
