Solution for April 2012

The Problem:
	Recall that the incenter $I$ of a triangle is the point where the three internal angle bisectors meet. Prove that any line through $I$ that divides the area of the triangle in half also divides its perimeter in half; conversely, any line through $I$ that divides the perimeter of the triangle in half also divides its area in half.

Correct solutions were submitted by

Lamis Alsheikh (Syria)	Diana Andrei (Sweden)
Luigi Bernardini (Italy)	Aleksandar Blazhevski-Cane (Macedonia)
Saturnino Campo Ruiz (Spain)	Bernard Collignon (France)
Hubert Desprez, (France)	Sébastien Dumortier (France)
Mei-Hui Fang (Austria)	Philippe Fondanaiche (France)
Verena Haider (Austria)	Tony Harrison (England)
Benoît Humbert (France)	Ile Ilijevski (Macedonia)
Matthew Lim (USA)	Patrick J. LoPresti (USA)
Raphaël Notarantonio (France)	Albert Stadler (Switzerland)
Arthur Vause (UK)

Our solution this month is quite short, but we will have lots to add about the problem.
Triangle geometry employs a notation that has become standard: Our triangle $ABC$ has sides $a = BC, b=CA$, and $c=AB$; its incenter is $I$, inradius $r$. We use square brackets to denote area. Let $\ell$ be an arbitrary line through $I$; because such a line must intersect two sides of $\Delta ABC$, we label the figure so that $\ell$ meets $AC$ at $D$ and $AB$ at $E$. Finally, let $b'=DA$ and $c'=AE$.

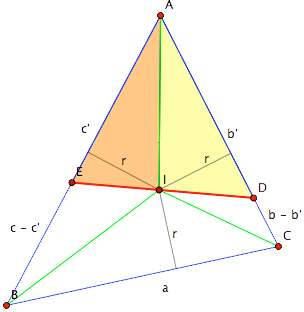
Our proof consists of eight equivalent statements.
\begin{eqnarray*}
\ell \mbox{ divides the area of} &\Delta&ABC \mbox{ in half }\\ &\Leftrightarrow& [ABC] = 2[AED]\\
&\Leftrightarrow& [ABI]+[BCI]+[CAI] =2\left([AEI]+[AID]\right)\\
&\Leftrightarrow& \frac{c \cdot r}2 +\frac{a \cdot r}2 +\frac{b \cdot r}2 =2\left(\frac{c' \cdot r}2
+\frac{b' \cdot r}2\right)\\
&\Leftrightarrow& a+b+c = 2(c' + b')\\
&\Leftrightarrow& a+(b-b')+(c-c') = b' + c'\\
&\Leftrightarrow&BC + CD + EB = DA + AE\\
&\Leftrightarrow& \ell \mbox{ divides the perimeter of $\Delta ABC$ in half.}
\end{eqnarray*}

Comments. Note that our argument remains valid should the point $D$ coincide with the vertex $C$, in which case $DI = CI$ bisects $\angle ACB$. As several correspondents observed, for the angle bisector $CE$ to divide either the area or perimeter of $\Delta ABC$ in half, $E$ would necessarily be the midpoint of $AB$, and the triangle would be isosceles with $CA = CB$.

Stadler kindly sent us a reference to a "Proof Without Words" [3] which proved pictorially that a line passing through the incenter of a triangle bisects the perimeter if and only if it bisects the area. Unfortunately, that proof badly needs quite a few words to become comprehensible; even then the argument there is not as simple as what we have featured above, which is a distillation of the lovely solutions sent in by our readers.

Stronger theorems. By arguing more carefully one can prove a result appearing in [2], namely

If any two of the following statements hold about a line $\ell$ that passes through a given triangle, then so does the third: (i) $\ell$ bisects the area of the triangle; (ii) $\ell$ bisects the perimeter of the triangle; (iii) $\ell$ contains the incenter of the triangle.

Verena Haider discovered a beautiful theorem which has the preceding results as immediate consequences.

Haider's Theorem. For any triangle $ABC$ and any line $\ell$, $\ell$ divides the area and the perimeter of $\Delta ABC$ in the same ratio if and only if it passes through the triangle's incenter.

Proof. We first assume that $\ell$ divides the area and the perimeter of $\Delta ABC$ in the same ratio. In our previous notation the ratio of areas is
$$\frac{[EBCD]}{[AED]} = \frac{[ABC]-[AED]}{[AED]} = \frac{[ABC]}{[AED]}-1,$$
while the ratio of perimeters is
$$\frac{EB+BC+CD}{DA+AE} = \frac{(c-c')+a+(b-b')}{b'+c'}.$$
The right-hand sides are equal when
$$ \frac{[ABC]}{[AED]} = 1 + \frac{(c-c')+a+(b-b')}{b'+c'} = \frac{a+b+c}{b'+c'},$$
or
\begin{equation}
[AED] = \frac{b'+c'}{a+b+c}[ABC] = \frac{b'+c'}{a+b+c}\cdot(a+b+c)\frac{r}2 = (b'+c')\frac{r}2.
\end{equation}
We want to prove that $I$ lies on $DE$; to this end we let the bisector of $\angle BAC$ meet $DE$ at $F$. The perpendicular distances from $F$ to $AC$ and $AE$ have the same value, say $d$. Therefore,
\begin{equation}
[AED]=[AEF]+[AFD] = \frac{c'd}2 + \frac{b'd}2 = (b'+c')\frac{d}2.
\end{equation}
Equations (1) and (2) imply that $d=r$. Because $I$ is the unique point on the angle bisector $AI$ at a distance of $r$ from $AB$ and $AC$, it follows that $F$ coincides with $I$, whence $I$ lies on $DE$ as claimed.

For the converse we are given that $I$ lies on $DE$. We start the chain of equalities with the ratio of areas,
\begin{eqnarray*}
\frac{[EBCD]}{[AED]} &=& \frac{[ABC]-[AED]}{[AED]}\\
&=& \frac{\frac{r}{2}\cdot(a+b+c)-\left([AEI]+[AID]\right)}{[AEI]+[AID]}\\
&=& \frac{\frac{r}{2}\cdot(a+b+c)-\left(b'\cdot\frac{r}2 + c'\cdot\frac{r}2\right)}{b'\cdot\frac{r}2 + c'\cdot\frac{r}2}\\
&=& \frac{(c-c')+a+(b-b')}{b'+c'} = \frac{EB+BC+CD}{DA+AE} ,
\end{eqnarray*}
and end with the ratio of the two pieces of the perimeter; that is, the two ratios are equal as desired.

Further comments.

• Let us call a line that simultaneously bisects the area and perimeter a bisecting line. Campo, Desprez, Fondanaiche, and Harrison all addressed the question of existence. To see that for any triangle there must exist a bisecting line, consider the family of lines $DE$ through $I$ as $D$ moves clockwise about the perimeter of the triangle. Define the function $f(D)$ to equal the quantity obtained by subtracting the area to the left of $DE$ (when looking from $D$ to $E$) from the area to the right. It is easy to see that $f(D)$ is continuous; moreover, its value for a particular point $D$ is the negative of the value when $D$ and $E$ have switched places. Somewhere between those two points is a position of $D$ for which $f(D)=0$, which is therefore a position where $DE$ bisects the area; because it passes through $I$ we know that it must also bisect the perimeter
  
  
• In fact, as Campo Ruiz and Desprez both showed, every triangle has exactly one, two, or three bisecting lines; no other values are possible. It is not too hard to prove this claim; see, for example, [2] and the references there.
  
  
• In a letter to the editor [6], Anthony Todd wrote that he learned of the bisecting-line problem from a 1994 article by A. Shen [4]. That article describes the discrimination against certain ethnic groups in entrance examinations to the Mekh-mat at Moscow State University during the 1970's and 1980's. One of the difficult problems designed to eliminate many of the targeted applicants was to draw a straight line that bisects the area and perimeter of a triangle. We have seen that showing the existence of such a line is quite easy; constructing that line is much harder. A solution to the harder problem can be found in [7], pages 19-20 and (in Spanish) by Campo Ruiz [1]. Todd's letter concludes by listing several interesting references; one, in particular, is his interactive web page [5] with an applet that displays the bisecting lines of an arbitrary triangle $ABC$ with fixed side $AB$; vertex $C$ is free to move about the plane. The applet indicates the regions in which the vertex $C$ must lie in order for one or three bisecting lines to appear, with their common boundary being the locus of $C$ for which two bisecting lines appear.
  

References

1. Saturnino Campo Ruiz, Solución Problema 138
   http://www.aloj.us.es/rbarroso/trianguloscabri/sol/sol138sat.htm.
   
   
2. Dimitrios Kodokostas, Triangle Equalizers, Mathematics Magazine, 83 : 2 (Apr. 2010) 141-146.
   
   
3. Sidney H. Kung, A Line through the Incenter of a Triangle, Mathematics Magazine, 75 : 3 (June 2002) 214.
   
   
4. Alexander Shen, Entrance Examinations to the Mekh-mat, The Mathematical Intelligencer, 16 : 4 (1994) 6-10; available at
   http://www.3038.org/press/shen.pdf.
   
   
5. Anthony Todd, Bisecting a Triangle,
   http://www.math.colostate.edu/info/applets/bisect_triangle/bisect_triangle.html
   
   
6. Anthony Todd, Letter to the Editor, Mathematics Magazine, 84 : 5 (Dec. 2011) 396.
   
   
7. Ilan Vardi, Mekh-mat Entrance Examination Problems, http://www.lix.polytechnique.fr/Labo/Ilan.Vardi/mekh-mat.html.