|
Solution for May 2012
| The Problem: |
 |
An arbitrary permutation $\sigma$ of the set of integers from 1 to 2012 can be represented in the plane by a set of 2012 points of the form $\left(k, \sigma(k)\right)$, where $k$ runs from 1 to 2012. The smallest square bounding this set of points with sides parallel to the coordinate axis has at least 2 and at most 4 points of the set on its boundary. Determine the number of permutations having exactly $m$ points on the boundary for $m$ equal to 2, to 3, and to 4.
To help you understand the problem, we include an example below of the corresponding figure for when $\sigma$ is a permutation of the numbers from 1 to 7 that has four points on its bounding square, namely the permutation that takes the ordered set $(1, 2, 3, 4, 5, 6, 7)$ to $(5, 3, 6, 1, 7, 2, 4)$.
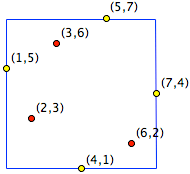
|
Correct solutions were submitted by
|
Lamis Alsheikh
(Syria) |
Diana Andrei (Sweden) |
|
Luigi Bernardini (Italy) |
Aleksandar Blazhevski (Macedonia) |
|
Bernard Collignon (France) |
Gruian Cornel (Romania) |
|
Mei-Hui Fang (Austria) |
Philippe Fondanaiche (France) |
|
Jan Fricke (Germany) |
Verena Haider (Austria) |
|
Tony Harrison (England) |
Benoît Humbert (France) |
| Ile Ilijevski (Macedonia) |
Matthew Lim (USA) |
| Raphaël Notarantonio (France) |
Mathias Schenker (Switzerland) |
| Albert Stadler (Switzerland) |
Arthur Vause (UK) |
| Wu ChengYuan (Singapore) |
|
Our problem this month is based on Mathematics Magazine's Problem 1861, proposed by Emeric Deutsch; we replaced the arbitrary integer $n \ge 2$ of Deutsch's problem with $n = 2012$. The solution to that problem appeared in Vol 85, No. 1 (February 2012) on page 63: Of the $n!$ points whose $x$-coordinate is an integer from 1 to $n$ and whose $y$-coordinate is $\sigma (x)$ for some permutation $\sigma$ of the $x$-coordinates, there will be
| 2 boundary points |
for $2(n-2)!$ of the permutations |
| 3 boundary points |
for $4(n-2)(n-2)!$ of the permutations |
| 4 boundary points |
for $(n-2)(n-3)(n-2)!$ of the permutations |
Although almost all of the solutions we received were for the general problem (for arbitrary $n$), we will give the answer only for the case $n=2012$. To obtain the general solution simply replace 2012 everywhere by $n$, 2011 by $n-1$, and so on.
Let $\sigma$ be a permutation of the numbers from 1 to 2012. For every integer $k$ from 1 to 2012, each vertical line $x=k$ contains exactly one point of our set, namely $(k, \sigma(k))$, while each horizontal line $y=k$ likewise contains exactly one point of the set, namely $(\sigma^{-1}(k), k)$. In particular, a point $(x, \sigma(x))$ lies on the left side of the smallest bounding square exactly when $x=1$, on the right when $x=2012$, on the top when $y = \sigma (x) = 2012$, and on the bottom when $y = \sigma(x) = 1$. In general these four boundary points will be distinct.
2 boundary points. A permutation $\sigma$ will determine two boundary points when the upper boundary point coincides with one of the vertical-side points, while the point on the other vertical side coincides with the lower boundary point; in other words, the two points must be located at opposite corners of the boundary square. The points will be at the corners $(1,1)$ and $(2012,2012)$ (that is, $\sigma(1)=1$ and $\sigma(2012)=2012)$) for $2010!$ of the permutations (because once $\sigma(1)$ and $\sigma(2012)$ have been fixed, we are left with permutations of the 2010 numbers from 2 to 2011). The same analysis is valid for the corners $(1, 2012)$ and $(2012,1)$, which makes a total of
$$\mathbf{2 \cdot 2010!} \mbox{ permutations with two boundary points.}$$
3 boundary points. There will be three boundary points if exactly one of them is at a corner. If the chosen corner is $(1,1)$ then there will be 2010 choices for $\sigma (2012)$ (namely, anything but 1 and 2012). That leaves $2010!$ choices for the remaining $2010$ values of $x$. This analysis applies similarly to all four corners for a total of
\[\mathbf{4 \cdot 2010 \cdot 2010!} \mbox{ permutations with three boundary points.}\]
4 boundary points. The number of permutations with four boundary points can be obtained by subtracting from $2012!$ the number of permutations already considered. Alternatively, we observe that there will be four boundary points if all four corner positions are avoided. To manage this we can choose any of the 2010 numbers from 2 to 2011 for $\sigma (1)$, any of the remaining 2009 numbers for $\sigma (2012)$, and any of the remaining $2010!$ assignments for the other values of $\sigma$. The total is therefore
\[\mathbf{2010\cdot 2009 \cdot 2010!} \mbox{ permutations with four boundary points.}\]
To check that our numbers make sense, we can add the three totals we have obtained:
\begin{eqnarray*}
2\cdot 2010! + 4 \cdot 2010 \cdot 2010! + 2010 \cdot 2009 \cdot 2010! &=&
(2+2013\cdot 2010) \cdot 2010!\\ &=& (2012\cdot2011) \cdot 2010! = 2012!,
\end{eqnarray*}
as expected.
|

