Solution for April 2013

The Problem:

Find all pairs $c$ and $d$ of real numbers such that all roots of the polynomials $$6x^2-24x-4c \quad \mbox{ and } \quad x^3 +cx^2 +dx - 8$$ are nonnegative real numbers. Answer. There exists a single pair of values for which all roots are nonnegative and real, namely $c = -6, d=12$. Lamis Alsheikh (Syria) Diana Andrei (Sweden) Jose Arraiz (France) Ricardo Bernabé Baloni (Argentina) Aleksandar Blazhevski (Macedonia) Radouan Boukharfane (Québec) Lou Cairoli (USA) Bernard Carpentier (France) Allen Druze (USA) Edgardo Figueroa Donayre Jan Fricke (Germany) Georges Ghosn (Québec) Tony Harrison (UK) Kipp Johnson (USA) Matthew Lim (USA) Patrick J. LoPresti (USA) Nawal Kishor Mishra (India) Luis Rivera Albert Stadler (Switzerland) Bruno Tisserand (France)   We also received three solutions that were incomplete and one that was incorrect.

The solution:

When $c=-6$ and $d=12$ the polynomials become $6(x-2)^2$ and $(x-2)^3$, whence all five roots coincide at $x=2$ and are thereby nonnegative and real. We must now show that there are no further satisfactory pairs. Everybody's first step was to consider the quadratic $f(x) := 6x^2-24x-4c$ and show that for its roots to be real we must have $c \ge -6$: either note that its discriminant is $24^2-4\cdot 6 \cdot (-4c) = 96(6+c)$, which is nonnegative exactly when $c \ge -6$; or write $f(x) = 6(x-2)^2 -4(c+6)$ and note that its minimum is $-4(c+6)$ at $x=2$, which is below the $x$-axis when $c \ge -6$. (The requirement that the roots of $f(x)$ be nonnegative is not required; this extra condition forces $c \le 0$, but we shall soon see that the given cubic is more restrictive.)

To analyze the cubic we have a choice of using calculus or using the inequality of arithmetic and geometric means.

The AM-GM inequality. If $r,s$, and $t$ are the roots of the cubic we have
$$g(x) := x^3 +cx^2 +dx - 8 = (x-r)(x-s)(x-t).$$
Comparing coefficients yields $r+s+t = -c$ and $rst = 8$. To apply the AM-GM inequality we must make use of the requirement that the roots be nonnegative; in fact, they are positive (because their product is 8). The inequality tells us that any three positive numbers $r,s,t$ satisfy
$$r+s+t \ge 3\sqrt[3]{rst},$$
whence $-c \ge 6$; that is, $c \le -6$. But we earlier determined that $c\ge -6$, from which we deduce that $c = -6$. It quickly follows that $r+s+t = 6 = 3\sqrt[3]{rst}$; therefore $r=s=t=2$ and $d=12$. Consequently, $c = -6, d=12$ is the only pair satisfying the given conditions.

A calculus argument. The submissions that avoided the AM-GM inequality all used calculus to some extent. Here is how Harrison argued. Because the second derivative is $g''(x) = 6x+2c$, the cubic curve $y=g(x) = x^3 +cx^2 +dx - 8$ has a point of inflection at $\left(-\frac13c, \; \frac2{27}c^3-\frac13cd-8\right)$ (where the second derivative is zero). Because $g'\left(-\frac13c\right) = d-\frac13c^2$, the line tangent to the curve at its inflection point has the equation
$$y-\left(\frac2{27}c^3-\frac13cd-8\right) = \left(d-\frac13c^2\right)\left(x+\frac13c\right),
\quad \mbox{ or }$$ $$ y= \left(d-\frac13c^2\right)x -\left(\frac1{27}c^3 + 8\right); $$
it therefore intersects the $y$-axis where $y=-\left(\frac1{27}c^3 + 8\right)$. Because we know that $c \ge -6$, we deduce that the $y$-intercept is at most $\left(\frac1{27}(-6)^3 + 8\right) = 0$. But we know that for our cubic $g(x)$ to have distinct positive roots, it must attain its relative maximum for some value of $x$ between $x=0$ and the inflection point, as in the accompanying diagram. Moreover, this maximum must lie below the line that is tangent to the curve at its inflection point; but we know that the inflectional tangent must have a negative slope, and we have seen that it lies below the positive $x$-axis, thus preventing the the curve from meeting the positive $x$-axis to the left of the inflection point. We are therefore led to conclude that the inflectional tangent must coincide with the $x$-axis. This forces $\frac1{27}c^3 + 8 = 0$ and, therefore, $c=-6$. Finally, the slope of the tangent, namely $d-\frac13c^2$, must be 0, so that $d = 12$, as claimed.

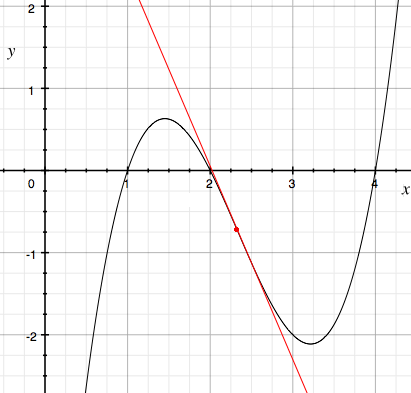
The graph of a cubic curve that has distinct positive roots,
shown with its inflectional tangent.

Acknowledgment. Our April problem was \#4 on the Estonian International Mathematical Olympiad Selection Contest 2004-2005. See Crux Mathematicorum 35:1 (February 2009) page 28.