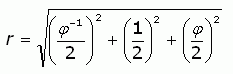| |||
| Math Central | Quandaries & Queries |
|
Question from ainslie, a student: Please help me with this problem A golden cuboid is defined as a rectangular prism whose lengh, width and hight are in the ratio of phi : 1 : 1/phi Prove that the ratio of the Surface Areas of the golden cuboid to that of the sphere that cicumscribes it is Phi : Pi. thank you |
Hi Ainslie.

You are asked to find the ratio (call it R) of the surface area of the cuboid to that of the sphere:
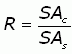
The formulas for the surface areas of the cuboid and the sphere are easy:
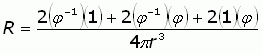
To find the surface area of the sphere, we will need to determine its radius r (you can see it represented faintly in the diagram.
Since r is also the distance from the geometric center of the golden cuboid to a corner, we can use the distance formula to find r.
Now you have all the pieces you need to assemble the solution, Ainslie. Substitute for r and simplify.
Hope this helps,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.