I am neither a math teacher nor a student, but I hope you will consider my question anyway. I recently was discussing repeated decimals with a friend, and went on the web to find out more about a pattern was looking for years ago. In doing so I came upon your correspondence on repeating decimals.

I often found, as a student, that mathematical and scientific explanations had a way of skipping quickly over the most essential element. In the present case, the core of the explanation is "Because there are at most 6 distinct remainders that can appear ({1,2,3,4,5,6})". My problem is that I don't see why that is obvious. Perhaps it will be clear to me in the morning. However, I'd be grateful if you could elaborate.

The pattern I referred to above has largely faded from my memory after 25 years or more, but it relates to the frequency with which the number of repeating decimals equals the divisor minus one, and similar frequencies for other special numbers. I hope to find something about this on the web.

Thanks for paying attention to this message.

-- Alan

To see this I think it helps to look at the "process" you learned when you learned to divide. Consider the example that is in the note you referred to above.

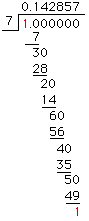
In the first step you divide 7 into 10 to give the first digit in the quotient as 1. 7x1 = 7, subtracted from 10 gives a remainder of 3. Bring down the 0. Now you have to decide what the next digit in the quotient will be.

• You could try 3. 7x3 = 21 and 21 subtracted from 30 is 9. But 9 is larger than 7 so 3 is too small. (Notice that you reject 3 since the remainder, 9, is too large.)
  
  
• You could try 5. 7x5 = 35 and 35 is larger than 30 so 5 is too large. (Here you reject 5 since the remainder is negative.)
  
  
• Now try 4. 7x4 = 28 and 28 subtracted from 30 is 2. Thus 4 is the correct, next digit in the quotient. (You accept 4 since the remainder is between 0 and 6.)

Thus, in the process of division, you only accept digits in the quotient if the remainder is 0, 1, 2, 3, 4, 5 or 6.

For help on the internet try looking under either "repeating decimal" or "repunit." The decimal expansion of a fraction continues to be a fascinating topic since it is so easliy understood and since many of its properties can be immediately seen or can be discovered witha little experminentation. The pattern of repeating digits are particularly intriguing. Why for example, does 3/11 = 0.2727... have two repeating digits while 3/7 = 0.428571428.. doesn't repeat until after the sixth digit? Although many such questions can be answered in a very elementary way, the topic is not trivial; it is enlightening for students to return to it at various stages of their mathematical careers. Some questions arise that are very difficult. For example, it is not known if there are infinitely many examples of prime numbers p for which 1/p repeats with the maximum period of p-1. Here are three references that have substantial elementary portions:

COLLEGE MATH. JOURNAL 15:4 (1984) pages 299-308.
COLLEGE MATH. JOURNAL 19:3 (1988) pages 240-246.
MATHEMATICS MAGAZINE 51:1 (1978) pages 22-28.