Hi my question is on linear programming My name is Sara i am a student in the12th grade and i need the answer to this problem so i know if i am doing it right or not. Here is the problem

A diet is to include at least 140 mg of Vitamin A and at least 145 mg of vitamin B. these requirements are to be obtained from two types of food. type X contains 10 mg of vitamin A and 20 mg of vitamin B per pound. Type Y contains 30 mg of vitamin A and 15 mg of vitamin B per pound. if type X food costs $12 and Type Y $8 per pound, how many pounds of each type of food should be purchased to satisfy the requirements at the minimum cost?

thanks soo much i need to know if i have the right answer and if i am doing it right because we have to do a presentation on it in class on Monday the 15th of jan. and our teacher wont help us or give us the answer so i ahve no clue if i am doing it right

thanks so much
sara

Suppose that the amount of type X food you use is P mg and the amount of type Y food you use is Q mg. Thus you get 10P + 30Q mg of vitamin A and 20P + 15Q mg of vitamin B. Hence the constraint equations are

You also have

Thus the constraint region is the region shaded in the diagram below.

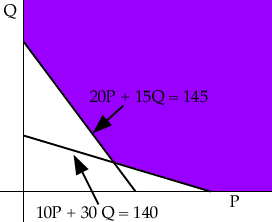
Now write an equation for the cost C,

This is a family of parallel lines, one for each value of C. Some of these lines will intersect the shaded region in the diagram above and some will not. The solution you want is the samllest value of C that will ensure that the line intersects the shaded region.

You may want to look at my solution to a similar problem.

Now to verify that you have the right answer, you use linear programing duality: Find a solution to the dual problem

If your answer is correct, you should get the same value in both cases.

The interpretation of the dual is the following: Suppose that I have vitamins A and B, and I want to sell it to a follower that follow that diet. I need to have a price a per mg of vitamin A and a price B per mg of vitamin B. I want to maximize my revenue of 140a + 145b. However, it should not be cheaper to buy food of type X than to get an equivalent supply of my vitamins, or I will not make a sale. In other words, I must respect the constraint 10a + 20b <= 12. Also, the food of type B should not be cheaper than an equivalent supply of vitamins: 30a + 15b <= 8.

In this way, what is my maximum revenue? It makes sense that it should be the same as the minimum cost of food that will satisfy the diet's requirement.