Hello,
I am a freshman engineer at the University of Michigan, but this question is in regards to a research project that I am working on. I don't quite know what "level" this is, but no one in my hall has been able to give me a satisfactory method to do this, so here goes. I have to calculate the areas of different "platts" of land from a map, and the only thing I have are the four side measures. There are some cases where no sides are parallel, no lengths the same, and no angles are given, and I was wondering how to calculate the area of such figures. I've attached a rough sketch of a typical platt's shape. Thank you for your time.

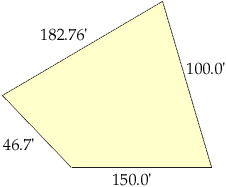
Steve

The simple answer is that you cannot calculate the area from this information - because the area is not determined by just the four edge lengths.

Conisder a paraellelogram with all sides 1. (Actually it is a rombus.) This might be a square - area 1. It might also be collinear (flat) area 0. Or any parallelogram in between - and therefore any area in between 0 and 1.

In general, to fix the area, the measurements (constraints) must be sufficient to make the figure 'unique up to congruence' or at least unique within a range of figures roughly described by a sketch or image.

For four points, the minimum number of such measurements (lengths, angles, diameters or diagonals etc.) is FIVE.

For N points the minimum is 2N-3 constraints. This fits with 3 measurements for a triangle, and one for a line segment ; - )

The people who study this work in general, work in areas like CAD programming, computational geometry, structural rigidity, etc.

Just knowing the correct number of constraints still leaves lots of room for other errors - and for some special situations where the calculation will fail (e.g. you will have an agorithm in which you now have to divide by 0 in the special case).

If you can measure a diagonal in the platt you have sketched above then you can calculate the area using Heron's Formula

Walter Whiteley