Who is asking: Other
Level: All
Question:
A math question concerning the area asked by Staci bounded by the chord of circle and the arc was answered by Harley with the following formula:
Area (S) = 1/2 (r2)theta
where r2 is the radius of the circle squared
where r = radius of the circle and theta is the angle in radians formed by the chord joined at its ends by radial lines.
A friend of mine is a farmer and uses Pivots to irrigate portions of his land. The crop rows are in straight lines that all form chords of a large circle. The intent is to determine area between any two "boundary" rows expressed in acres.
I attempted to apply the above formula using the following numbers
Circle radius = 1325 feet
Perpendicular distance from circle center to the chord is 1285 feet
theta was calculated to be 1.13091
(using the 1285 as one side of a right triangle, solving for its angle and then doubling the result to get theta)
Using the above formula, the acreage was calculated to be 22.78987374
(43560 square feet = one acre)
Since an annulus of a circle bounded between radii of 1285 and 1325 feet was earlier calculated to be 7.52 acres, the above result seems inconsistent.
Please advise what I need to do to get a good result in case you do not find my answer to be correct.
(note: computing intermediate rows would be accomplished by subtracting the area of the "outer" section from an overall calculation that includes the outer and a larger inner section)
Thanks,
Chuck
Hi Chuck,
I don't have clear in my mind what you mean by the area between two boundary rows so let me know if I am not finding the correct area. Here is the diagram I have.
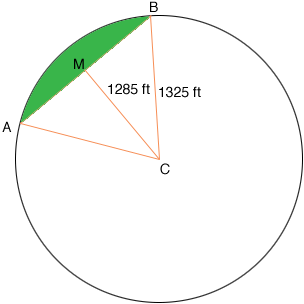
M is the midpoint of the chord BA so the angle BMC is a right angle. Let the angle ACB be t radians then |MC|/|CB| = cos(t/2) and hence
t = 2
cos-1(1285/1325) = 0.4927 radians
Hence the area of the sector CAB is
1/2
r2
t = 1/2
13252
0.4927 = 432481.44 square feet
which is 9.928 acres.
Since triangle BMC is a right triangle, Pythagoras' theorem tells us
|BM|2 + 12852 = 13252
and hence
|BM| = sqrt[13252 - 12852] = 323.110 feet.
Hence the area of the triangle BAC is
1/2
base
height = 323.110
1285 = 415196 square feet
which is 9.532 acres.
Thus the area of the region shaded green in the diagram is
9.928 - 9.532 = 0.396 acres
Harley