Here is my math question: A plot of land has the following dimensions: 391 ft. x 757 ft. x 208 ft. x 788 ft. Q: How many acres is this?
How was the calculation done?
Thank you!!!
Hi John,
It is possible to have many different shaped lots, all of which have the dimensions you sent, with quite different areas. Thus, just knowing the dimensions does not allow me to calculate the area. A more complete explanation is given in the answer to a previous question.
To get an idea of how much difference there might be in the areas I drew a diagram of what I think might be the shape of your lot.
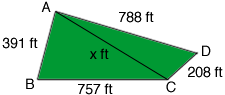
I then drew a diagonal from A to C to divide the lot into two triangles. I don't know the length of this diagonal so I called it x ft. (If I knew the value of x I could calculate the area of your lot.) I then used Heron's Formula to find the ares of the two triangles. Heron's Formula uses the lengths of all three sides so each of these expressions has the unknown x in it. I then added the areas of these triangles to get an expression for the area of your lot. I am going to call this expression f(x).
What can x be? An examination of Heron's Formula expressions for the areas of the two triangles shows that x can be any number between 580 ft and 996 ft. To get an idea of what values are possible for the area I plotted the area of the lot against x for x from 580 ft and 996 ft.
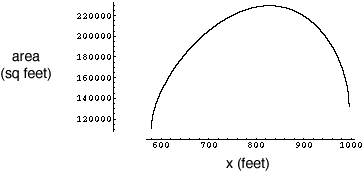
As you can see the area is something less that 120,000 square feet if x is 580 feet and a maximum of somewhat more than 220,000 square feet if x is a little over 800 feet. I then used calculus to find where this maximum appears and it is when x is 828.375 feet.
The calculations then show that a lot with the dimensions you sent can have an area of anywhere from 111,439 square feet or 2.6 acres if x is 580 feet to 229,427 square feet or 5.3 acres if x is 996 feet.
Harley