Subject: Hexagon Area
Name: Ashish
Who are you: Student

Dear Sir/Madam,
I want to find out area of an irregular HEXAGON in square feet, whose sides are as follows,
Side 1 = 60.6 Feet
Side 2 = 44 Feet
Side 3 = 41 Feet
Side 4 = 14 Feet
Side 5 = 21 Feet
Side 6 = 27.6 Feet
I will be grateful to you, if you kindly help me out.

Regards,

Ashish

Hello Ashish.

This earlier question describes why just providing the lengths of the sides of an irregular polygon isn't enough information to determine the area. You'll need to provide more measurements, such as the length of at least three diagonals or several angles.

Stephen La Rocque.>

Ashish wrote back

Dear Sir/Madam,

I want to find out area of an irregular HEXAGON in square feet,
whose sides are as follows,
Side 1 = 60.6 Feet
Side 2 = 44 Feet
Side 3 = 41 Feet
Side 4 = 14 Feet
Side 5 = 21 Feet
Side 6 = 27.6 Feet
Diagonal between (Side 1, Side 2) and (Side 3, Side 4) is 64.6 Feet
Diagonal between (Side 1, Side 2) and (Side 4, Side 5) is 72 Feet
Diagonal between (Side 1, Side 2) and (Side 5, Side 6) is 68 Feet

I will be grateful to you, if you kindly help me out.

Regards,

Ashish

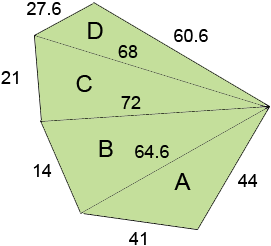
Thanks Ashish,

I drew a diagram (not to scale) of an irregular hexagon and added your lengths in feet.

The point of the diagram is to see that the diagonals divides the hexagon into four triangles which I have labeled A, B, C, and D. The area of the hexagon is then the sum of the areas of the four triangles.

The area of each of the triangles can be found using Heron's formula. For a triangle with sides of length a, b, and c let s = (a + b + c)/2. Heron's formula is then

area of the triangle = sqrt(s (s - a) (s - b) (s - c)) where sqrt is the square root.

For the triangle A in the diagram I got

s = (44 + 41 + 64.6)/2 = 74.8 feet
area of triangle A
= sqrt(74.8 (74.8 - 44) (74.8 - 41) (74.8 - 64.6))
= sqrt(794271.88) = 891.22 square feet

Using the same technique I found

Thus the area of the hexagon is 2843.3 square feet

Penny