Huw,

Your question is very much like the question that Daryl asked a while ago.

I drew a diagram and labeled some points. The dimensions are in centimeters.

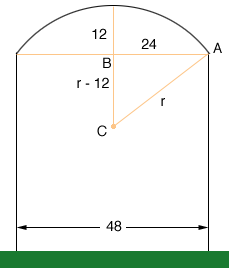
C is the centre of the circle that forms the arc and r is its radius. The triangle ABC is a right triangle, the length of AB is 24 cm, half the width of the arch, and the length of BC is r minus the the height of the arc above the top of the posts, which you want to be 12 cm. Thus, using Pythagoras' theorem

(r - 12)² + 24² = r²

Expanding gives

r² - 24r + 144 + 576 = r²

and hence

24r = 720 so that r = 720/24 = 30 cm.

Hence the length of BC is 30 - 12 = 18 cm and the angle BCA is cos^-1(18/30) = 0.9273 radians.

The length of an arc is r θ where θ is the angle that subtends the arc, measured in radians. Thus the length of half your arc is 30 0.9273 = 27.82 cm. Hence the arc at the top of your arch measures
2 27.82 = 55.64 cm.

I hope this helps,
Penny