| |||
| Math Central | Quandaries & Queries |
|
I have been looking at your site, but I am still confused as to how to figure out the exact square footage of my irregular lot (since it is a gradual fan lot from the front, and triangles out in the back). I am including the measurements as well as the Property Plot Map (parcel number 25). These appear to be the Measurements: Front: 71.22 Left Side: 180.87 Back left Corner: 17 Back: 101.35 Right Side: 151 Thank you so much for your help. Sincerely, Karyn |
Hi Karyn,
I can find an approximation of the square footage of your lot which is based on the assumption that the diagram you sent us is approximately to scale. I added some labels to the diagram so that I can refer to it.
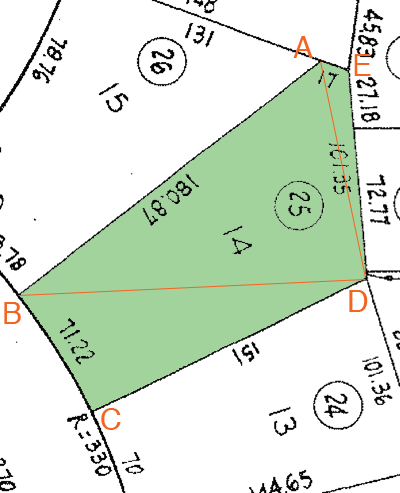
I need to find the lengths of BD and DA and this is where I need to assume that the drawing is approximately to scale.
I printed the diagram after turning off any scaling on my printer. I then measured the lengths of AB, CD and DE in Centimeters as accurately as I could. Her is what I found.
| Length (ft) | Measurement (cm) | Scale factor (ft/cm) | |
|---|---|---|---|
| AB | 180.87 | 10.1 | 180.87/10.1 = 17.91 |
| CD | 151 | 8.1 | 151/8.1 = 18.64 |
| DE | 101.35 | 5.6 | 101.35/5.6 = 18.10 |
These three scale factors should be the same. They are not but they are close so I found their average, 18.22 ft/cm and used it as a scale factor in order to approximate the lengths I need.
I next measured the lengths of BD and DA in centimeters on the diagram and multiplied each by 18.22 to approximate the lengths on your lot. I found the length of DB to be 167.59 feet and the length of DA to be 107.47 feet.
I then saw the lot as the quadrilateral ABCD and the triangle ADE. The area of the quadrilateral I found using the tool that Steve wrote. The calculated area is 14214 square feet. I then calculated the area of the triangle ADE using Heron's formula and found it to be 825 square feet. Thus my approximation of the area of your lot is 14214 + 825 = 15039 square feet.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.