The area of a property - Math Central

HOME

Math Central

Quandaries & Queries

Question from Mary:

I currently have an opportunity to sell my property to a business and they would like me to send a proposal to them with details.
I need to know the square footage of my property and have tried using your formula from similar questions. The dimensions of my property are as follows
front line facing street: 19.908 m
right side : 37.338 m
back line : 29.779 m
left side : 43.983m
The front line and the right side are at right angles to each other.

Can you formulate and reply? Thank you Mary

Hi Mary,

On my rough sketch of your property I added a diagonal to subdivide the property into two triangles.

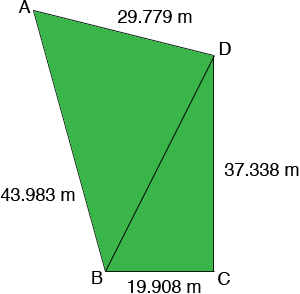
property

Since the angle at C is a right angle the area of triangle DBC is

1/2 base × height = 19.908/2 × 37.338 = 371.662 square metres.

To find the area of triangle ABD I need to find the length of the diagonal BD which I can do using Pythagoras' Theorem on the right triangle DBC.

|DB|² = 19.908² + 37.338² = 1790.4547 so |DB| = √1790.4547 = 42.314 metres.

Now that I know the lengths of all three sides of triangle ABD I can use Heron's Formula to find its area. I got the area of triangle ABD to be 602.049 square metres. Thus the area of your property is 371.662 + 602.049 = 973.711 square metres.

If you really want the area in square feet you can ask Google to make the conversion. Type the phrase

973.711 square meters in square feet

into the Google search engine and it returns

973.71100 (square meters) = 10 480.938 square feet

Harley

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.