Hi Matthew,

We are going to assume you mean a regular polygon. We can show you one approach that relies on some trigonometry. The crucial fact we need is that for x between 0 and π/3, tan(x) > x where the angle x is measured in radians. You can see this if you look at the graphs of f(x) = x and g(x) = tan(x).

Suppose you have a circle of radius r and perimeter p then

p = 2 r

and the area of the circle is

A_c = r²

Solve the first equation for r and substitute into the second to obtain

A_c = p²/(4 )

For a regular polygon with perimeter p and n sides join an adjacent pair of vertices A and B to the centre of the polygon C. Let Q be the midpoint of the edge AB.

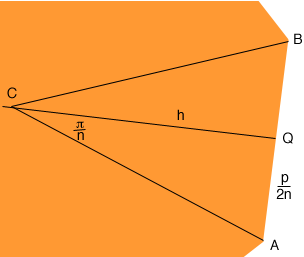
Diagram 1

Since the regular polygon has n sides and perimeter p the length of AB is p/n and thus the length of AQ is p/(2n). Again since the polygon is regular the measure of the angle BCA is 2 π/n radians and thus the measure of angle QCA is π/n radians. The distance from C to Q is the height h of the triangle BCA and

p/(2n) = h tan(/n)

The area of triangle BCA is half the base times the height which is

p²/[4 n² tan(/n)]

The polygon is composed of n such triangles and hence the area of the polygon is

A_p = p²/[4 n tan(/n)]

I am going to use a table to compare A_c and A_p.

Ac	inequality	Ap
p2/(4 )	?	p2/[4 n tan(/n)]	Multiply both columns by 4/p2
1/	?	1/[n tan(/n)]	Multiply both columns by [π n tan(π/n)]
n tan(/n)	?		Divide both columns by n
tan(/n)	>	/n

Since n must be 3 or larger to form a polygon we know that tan(/n) > /n.

Now step through the table from the final row to the first row. Each multiplication and division is by a positive quantity and hence the direction of the inequality at each step is unchanged so we can conclude that A_c > A_p.

Stephen and Penny

Matthew wrote back

Thank you for answering my question before about why a circle has a larger area than any other polygon. Unfortunately, I could not understand it. PLEASE can you explain it to me again simpler.
Thanks

Matthew,

This is not an easy problem and I am not sure I can show you a simpler answer. I can show you another approach but it again comes down to showing tan(/n) > /n where the angle measurement is in radians.

Start by drawing a regular polygon with n sides, each side of length a metres. Let C be the centre of the polygon. Draw a circle with centre C that has the same area as the polygon as in the diagram.

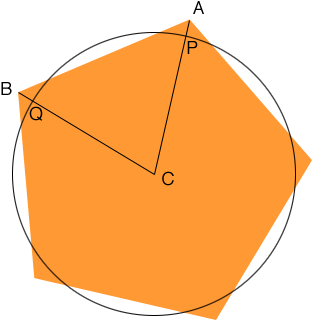
Diagram 2

The perimeter of the polygon is n times the distance from A to B. The perimeter of the circle is n times the length of the arc from P to Q. If I can show that the length of the line segment AB is greater than the length of the arc from P to Q then to force the circle and polygon to have the same perimeter I would need to shrink the polygon and hence reduce its area. Thus if the circle and the polygon have the same perimeter then the circle has a larger area.

Proof that the length of AB is larger than the length of the arc PQ.

We started with circle and polygon in the diagram having the same area. Recall that the length of AB is a. Furthermore the perimeter of the circle is 2 r and thus the length of the arc PQ is 2 r/n.

The area of the circle is r² and, according to Sue's answer to an earlier problem, the area of the polygon is a² n/[4 tan(/n)]. (again recall tat I am using radians for the angle measurements.) Thus

r² = a² n/[4 tan(/n)]

Solving for a² gives

a² = [4 r²/n] [tan(/n)]

As I said at the outset the necessary fact is that

tan(/n) > /n

Multiply both sides by 4 r² /n

4 r² /n tan(/n) > 4 r^{2 2}/n²

From above the left side is a² and hence

a² > 4 r^{2 2}/n²

Finally take the square root of both sides to get

a > 2 r/n

But the right side is the length of the arc PQ so I have shown that the length of the line segment AB is larger than the length of the arc PQ.

I hope this helps,
Penny

Thank you very much for your help on showing why a circle has a larger area than any polygon with the same perimeter. I am really starting to understand it now, however there is just one bit I am struggling with.
Can you please explain to me where you got tan(pi/n) from?
This would be a great help and greatly appreciated.
Thanks
Matthew

Matthew,

Look at diagram 2 above. The polygon has 5 sides so if you join each vertex to C you will form 5 congruent triangles. Since the angle at C, all the way around the circle measures 360^o, the angle ACB has measure 360^o/5. In a similar way if the polygon had n sides then the measure of the angle ACB would be 360^o/n.

Now look at diagram 1. Again the measure of the angle ACB is 360^o/n and hence the angle ACQ has measure 180⁰/n. But I am measuring the angles in radians rather than degrees and there are radians in 180^o. Thus the angle ACQ has measure /n radians.

Does that help?

Penny