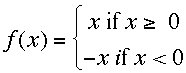Hi Moulipriya,

Let f(x) = |x|. I want to start by writing f(x) a different way that doesn't use the absolute value notation. Since |x| = x if x is positive or zero and |x| = -x if x is negative I can write

You can find a graph of this function in the answer to a previous question.

The definition of continuity of a function g(x) at a point a involves the value of the function at a, g(a) and the limit of g(x) as x approaches a. Thus the continuity at a only depends on the function at a and at points very close to a. Hence for f(x) = |x|, if a > 0 then close to a the function is given by f(x) = x which is continuous and if a < 0 then close to a the function is given by f(x) = -x which is also continuous. Thus the only point where f(x) = |x| might not be continuous is a = 0.

Look at the definition of continuity and apply it to f(x) = |x| with a = 0. To evaluate the limit you will need to consider two cases, the limit as x approaches 0 from the right and the limit as x approaches 0 from the left.

I hope this helps,
Penny