Steve,

Unfortunately there isn't enough information here to find the area of your lot. Besides the lengths of the sides I need some information on the shape of the lot. If you can tell me the angle at one of the corners or the length of one of the diagonals then I can find the area.
There is more information at mathcentral.uregina.ca/QQ/database/QQ.09.03/dave1.html

Harley

Steve wrote back.

715 length by 479.42 with (90degree angle), by 582 length by 477.18 .

Using your description I drew a rough diagram (not to scale). You didn't give me units so I am going to assume they are feet. I labeled the corners so that I can refer to them.

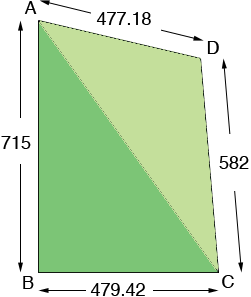
The angle at B is a right angle so I can find the area of the triangle AC using the fact that the area of a triangle is half the base times the height. Thus I get

area of triangle ABC =  ^479.42/₂ 715 = 171392.65 square feet.

Again since triangle ABC is a right triangle I can use Pythagoras theorem to find the length of AC.

|AC|² = 715² + 479.42² = 741068.54 and hence |AC| = 860.85 feet.

Now that I have the lengths of all three sides of triangle ACD I can find its area using Heron's formula. I got

area of triangle ACD = 131817.21 square feet.

Thus the area of your lot is

171392.65 + 131817.21 = 303209.86 square feet.

There are 43560 square feet in an acre so the area of your lot is

303209.86/43560 = 6.96 acres.

Harley