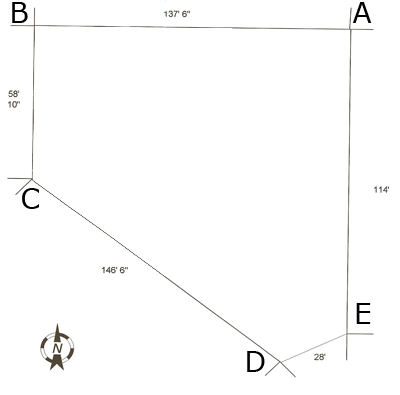
I have been trying to calculate the square footage of my property, without success. The measurements are below.

Is there a simple formula that can be used based upon the outside parameters? Or, is there a simple way to calculate the square footage? Please help, I have trying to solve this for about two weeks off and on, any help would be greatly appreciated.

Thanks
Jack


South to north (east side) = 114'
East to west (northside) = 137' 6"
North to south (westside) = 58' 10"
West to Southeast (southside) = 146' 6"
South to northeast (southside) = 28'

Hi Jack. There's no simple formula based only on the outside lengths.

That's because the outside lengths alone don't tell enough about the shape. See this earlier question for more information. From the diagram you sent us however it may be possible to calculate the area. Are the angles at A and B right angles? I am going to assume they are and show you how to find the area in this situation.

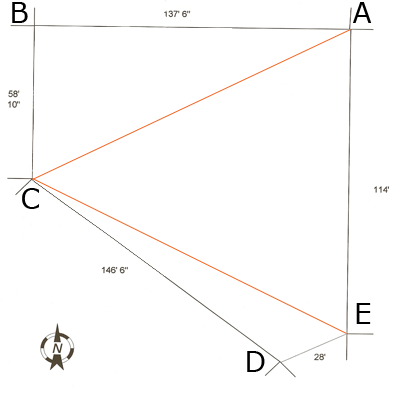
First join the points A and C and C and E to subdivide your property into three triangles.

Since the angle at B is a right angle the triangle ABC is a right triangle and hence Pythagoras theorem

|AC|2 = |AB|2 + |BC|2

gives |AC| = 149.56 feet.

The tangent of the angle CAB is |BC|/|AB| and hence the measure of the angle CAB is tan-1( |BC|/|AB|) = 23.16 degrees. Since the angle EAB is a right angle

angle EAC = 90 - 23.16 = 66.84 degrees.

Now you can use the law of cosines with the triangle ACE. This is

|CE|2 = |AE|2 + |AC|2 - 2 |AE| |AC| cos(EAC)

This gives |CE| = 148.16 feet.

The area of your property is the sum of the areas of the three triangles. Triangle ABC is a right triangle so AB is the base then |BC| = 58.833 feet is the height and you can find its area using

triangle area = 1/2 base x height.

For the other two triangles you can find the areas using Heron's formula.

Stephen and Penny