Subject: area of a 20 sided shape
Name: Kate
Who are you: Student

could you please tell me the strategy of how to work out the area of a 20 sided polygon thanks

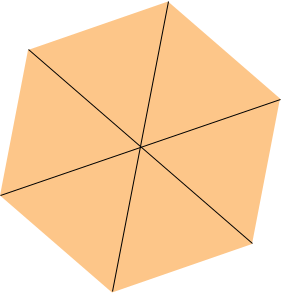
Hi Kate.

Assuming you mean a 20-sided regular polygon (one in which all sides are equal and all angles are equal), then the best strategy I know of is to subdivide the figure into 20 congruent isosceles triangles by joining each vertex to the center. Because you've divided the original figure into 20 congruent triangles, you know the central angle. We have included a diagram for a 6-sided regular polygon.

From one of these triangles, you can calculate the area by subdividing further into two congruent right triangles. The length of one leg is half the length of one side of the polygon. Use the tangent function to find the length of the other leg (the hypotenuse is the radius, but you may not need that). Then the area is 40 times the area of the small right triangle for which you already have the height and width.

Even if your 20-sided polygon is not regular you can use this technique of dividing the region into triangles. There is an example of an irregular hexagon in the answer to a previous question.

Hope this helps,
Stephen and Penny.