Hello Chetna. This is an interesting geometry problem.

This is indeed a little different from knowing the radius of the pentagon (or rather the circle circumscribing it).

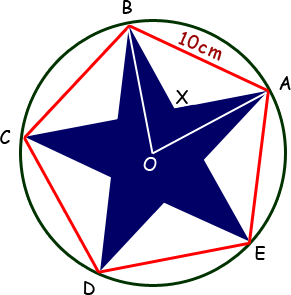
Take a look at the diagram on the right. Satisfy yourself through inspection that the blue area enclosed by the shape OAXB is exactly one-fifth of the total blue area. Thus we can find the area of this shape and multiply by five to find the area of the star.

Due to symmetry, I am sure you will agree that OB = OA (the radius of the circumscribing circle) and BX = AX.

Thus, we are talking about the areas of isosceles triangles.

We know the angles involved as well. The total of all the interior angles of any polyhedron is 180° + 180° × (sides-3). So for the red pentagon, this is 540°. Since this is a regular pentagon, all the interior angles are the same: 540°/5 = 108°. Since OB bisects angle ABC, we know that angle ABO = angle OAB = 54°.

Keep applying this procedure and you can quickly find that angle BXA must be 108°. I'll leave it to you to confirm this with your own calculations.

Of course, in triangle OAB, we compute angle BOA as 180° - 2 × 54° = 72°.

So we know:

1. area of the star = 5 times area of quadrilateral OAXB.
2. area of OAXB = area of triangle BOA - area of triangle BXA.
3. area of triangle BOA = area of an isosceles triangle with base 10 cm and vertex angle 72°.
4. area of triangle BXA = area of an isosceles triangle with base 10 cm and vertex angle 108°.

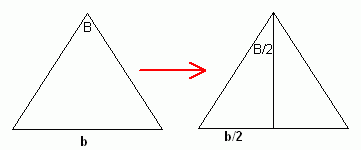
Starting with any isosceles triangle with base b and vertex angle B, let's find the area. The area of a triangle is 1/2 the base times the height, so we need the height of the isosceles triangle.

If we bisect angle B, the bisector will bisect the base at a right angle, so we have a right triangle problem.

The other leg of this right triangle is the height of the triangle. It can be found using the tan (tangent) function: height = (b/2) / tan(B/2).

Thus the height of the isosceles triangle is known and so the area of any isosceles triangle whose base is b and whose vertex angle is B can be calculated as:

A = (1/2) (b) [ (b/2) / tan(B/2) ] = b² / [ 4 tan (B/2) ]

Since you know b and B for your two isosceles triangles, this solves the question. I'll leave it to you to put the numbers into your calculator to complete the question.

Hope this helps,
Stephen La Rocque.