 |
| ||
| |||
|
| Math Central | Quandaries & Queries |
|
Im trying to form a hexagonal pyramid out of plywood and need to know the height to the center point of the pyramid. I want to use standard 4x8 sheets of plywood and split them diagonally. Then with the resulting triangles combine them to form one triangle. Then i want to accumulate 6 of these triangle total and put together to form a hexagonal pyramid. |
Hi David.
I'll draw one of the triangles on a sketch and label some useful lines and points:
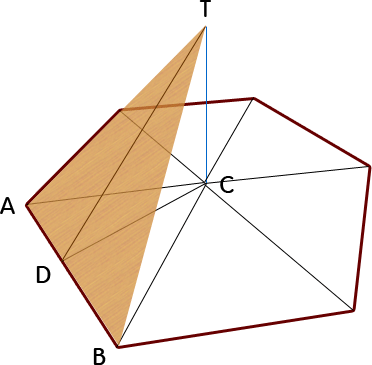According to your plan, AD should be 4 ft and DT should be 8 ft. Therefore AB is also 8 ft.
The length CT is what you want to find.
All the way around a full circle is 360°. Therefore because of symmetry, 
BCA must be 360°/6 = 60°. Since AC = CB by symmetry, that means all the angles of 
BCA are 60, so it is equilateral making AC also equal 8 ft.
If AC is 8 ft and AD is 4 ft, using the Pythagorean Theorem, CD2 = 82 - 42.
But if you look at DCT, it is also a right triangle, so DT2 = CD2 + CT2. This means that
CT2 = DT2 - CD2.
But that just means
CT2 = 82 - (82 - 42) = 42.
So CT, the height of the pyramid is 4 ft.
Hope this helps,
Stephen La Rocque.
PS: If you are interested in the angles to cut, then check this earlier question Chris and Harley answered.
| ||
| ||
| ||
 |
 |
|
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.