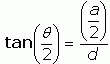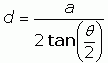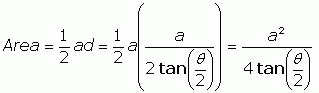Hi Josh. I presume you mean this question.

This is a drawing of an isosceles triangle ABC in which I've labelled an additional point and the lengths as well.

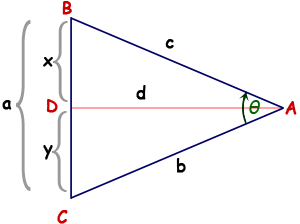The vertices are A, B, C, D in capital letters, the lengths are a, b, c, d, x, y in small letters.

I've bisected angle A, so DAB = CAD = θ/2. Since it is isosceles, c = b . Also, since it is isosceles, angles B and C are congruent.

Now consider the two triangles DBA and CBD. They have two angles we've proven congruent, so they are similar by the Angle-Angle Similarity Postulate. As well, they share a common corresponding side, so they are congruent. This means all the angles and sides are congruent as well.

So x = y = a/2 and the angles at D must be right angles, because they are supplementary.

Thus, by bisecting any isosceles triangle, we have proven that we divide it into two congruent right triangles.

In the earlier question, the only known values are a and θ. To get the area of the isoceles triangle, we can use the formula Area = ½base×height. We can say a is the base (turn your head) and d is the height. To get d, we can use the Tangent function from trigonometry:

Therefore we can substitute in what we know: x is a/2 and DAB = θ/2.

Now solve for d:

And put this into the area formula:

Q.E.D.

Stephen La Rocque.>