|
 |
|
Subject: Star of Bethlehem I need to construct a star for a Christmas play being done at our church. I want it to be a four-pointed star. The top and side points should be 12 inches long and the bottom point 24 inches. It will be flat on the back but raised on the front with lights inside for illumination. Each point will be made of two triangles with a ridge in the center. I would like the width of the rays at the center (widest point or center of star) to be about five inches and the center ridge at this same point to be raised about two inches from the flat back. I need to know the dimensions and angles of each of the 8 triangles that make up the star so that all of them meet properly at the center of the star so as to have the correct height from the flat back.
|
|
Hi Stephen, We had a similar question some time ago from Kent but for a five pointed star. I think you might find it enjoyable to see what he asked and the final product he produced. I made a paper model (not to scale) of three of the points of your star and labeled some points. You will see that I made "kite shaped" pieces rather than triangles. That is what Kent used and I find them easier to handle.
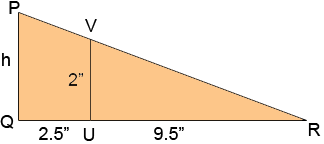
P is on the star at the highest point above the floor and Q, S, T and R are on the floor. Q is directly below P. From your description I have the distance from S to T to be 5 inches. Consider the triangle PQR.
U is the point where the line segments ST and QR meet and angle VQR is a right angle. According to your description the length of VU is 2 inches, |QR| = 12 inches and |QV| = 2.5 inches. Triangles PQR and VUR are similar and hence
thus
By Pythagoras' Theorem |PR|2 = h2 + 122 and thus
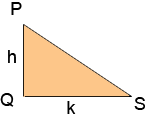
Now consider triangle PQS.
h = 2.526 inches and k = 2.5
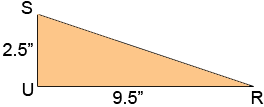
Finally consider triangle SUR.
Again this is a right triangle so
Thus the triangle you want to use, SPR has sides of length
I would not use angles to construct this triangle. I would draw the line segment PR of length 12.26 inches and then with a compass with point at P and distance between the point and the pencil of 4.33 inches draw an arc at approximately where you think S is located. Then set the distance between the compass point and pencil at 9.82 inches set the point at R and draw an arc to intersect the arc previously drawn. The intersection of the two arcs is the point S. For the remaining point of the star repeat the above calculation with |QR| = 24 inches. I don't know what material you arre planning to use but I would make a paper model first. Penny |
 |
 |
 |