Hi Jay,

We drew this diagram from your description:

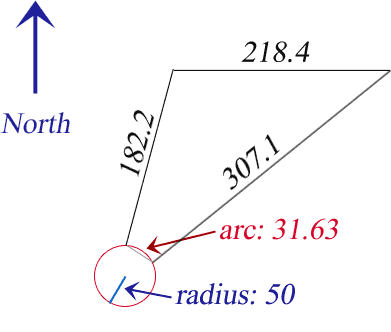
We've presumed that the 31.63 measurement is the length of the arc, rather than the straight line joining the two corners. Most surveys measure the lengths of property lines, and we suspect that's where your figure comes from.

The way to tackle this is in pieces. Watch as I divide the shape up and define some vertices for referencing. The green lines are north-south lines:

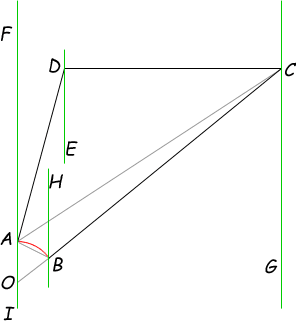
The area of your property equals:

    The area of quadrilateral ABCD (straight lines)
MINUS
    the area of the circular segment AB.

So let's break this up further:

The area of quadrilateral ABCD equals:

    The area of triangle ABC
PLUS
    the area of traingle ACD.

And the area of circular segment AB equals:

    The area of circular sector AOB
MINUS
    the area of isosceles triangle AOB.

So when we put all this together, we want:

(aACD + aABC) - ( aAOB - aAOB)

So let's take this piece by piece.

Area of Triangle ACD:

Angle FAD is given as 15°1′22″ and therefore angle ADE is also (alternate interior angles).
Angle EDC is given as 89°46′26″.
Angle ADC is the composite of EDA and EDC, so ADC = 15°1′22″ + 89°46′26″ = 104.783°.

Since we know the lengths of AD and CD and the angle ADC, we can use the law of cosines to calculate the length of AC:

AC² = AD² + CD² - 2(AD)(CD)cos(ADC)
AC² = 182.2 ² + 218.4² - 2(182.2)(218.4)cos(104.783°)
AC = 318.1 ft.

Now that we know the lengths of all three sides, we can use Heron's Formula to calculate the area of the triangle:

s = ½(AC + CD + AD) = ½(318.1 + 218.4 + 182.2) = 359.35.
(aACD)² = s (s - AC)(s - CD)(s - AD)
(aACD)² = 359.35 (359.35 - 318.1)(359.35 - 218.4)(359.35 - 182.2)
aACD = 19238.6 ft².

Area of Triangle ABC:

Angle EDC is given as 89°46′26″ and angle GCD iits supplementary angle (adjacent interior angles), so angle GCD is 180 - 89°46′26″ = 90°13′34″.
Angle GCB is given as 51°16′21″, so I can subtract that from GCD to get the angle BCD, thus angle BCD = 90°13′34″ - 51°16′21″ = 38°57′13″.

I want angle BDA, but to get that from BCD, I need to subtract angle ACD, which I don't know. But using the law of sines, I can get it from triangle ACD.

(AC) / sin(ADC) = (AD) / sin (ACD)
ACD = sin^-1 (AD / (AC / sin(ADC) ) )
ACD = sin^-1 (182.2 / (318.1 / sin(104.783°) ) ) = 33.629°.

Now I can calculate angle BDA: 38°57′13″ - 33.629° = 5.325°.

Thus I again have two side lengths and the included angle, so I can calculate the length of straight side AB using the law of cosines:

AB² = AC² + BC² - 2(AC)(BC)cos(BDA)
AB² = 318.1² + 307.1² - 2(318.1)(307.1)cos(5.325°)
AB = 31.06 ft.

Now that we know the lengths of all three sides, we can use Heron's Formula again to calculate the area of the triangle:

s = ½(AC + AB + BC) = ½(318.1 + 31.06 + 307.1) = 328.13.
(aABC)² = s (s - AC)(s - AB)(s - BC)
(aABC)² = 328.13 (328.13 - 318.1)(328.13 - 31.06)(328.13 - 307.1)
aABC = 4534.4 ft².

Thus the area of the quadrilateral (ignoring the tiny curved area) is 4534.4 + 19238.6 = 23773 ft². At 43560 square feet to the acre, this is equivalent to 0.546 acres.

Area of Sector AOB:

Angle AOB is congruent to angle GCB, which was given as 51°16′21″.
The sector is cut from a 50 ft radius circle. The full circle's area would be π(50²). However, we just want a portion of it. Since a full circle is 360 degrees, the area of the sector is:

aAOB = π(50²) ( 51°16′21″ / 360°) = 1118.6 ft².

Area of Isosceles Triangle AOB:

The area of an isosceles triangle, given the length L of the common side and the vertex angle V, is given by the formula:

Area = L² cos ( V / 2 ) sin ( V / 2 )

(We could also have done this using right triangles with more trig, but let's just use the formula for this.)

So we have

aAOB = (50)² cos ( 51°16′21″ / 2 ) sin ( 51°16′21″ / 2 ) = 975.2.

Thus, the area of the little circular segment AB is 1118.6 - 975.2 = 143.4 ft².

Subtracting this from the quadrilateral, we get

23773 - 143.4 = 23629.6 ft2 = 0.542 acres.

and that would be the area of your property.

Cheers,
Stephen La Rocque and Harley Weston.