Hi Jerry,

Is this what you are planning to do, where r = 553/2 = 276.5 mm? The cone may be pointed outside the cylinder but the calculations are the same. If so you need to decide what you want as h, the height of the cone in millimeters.

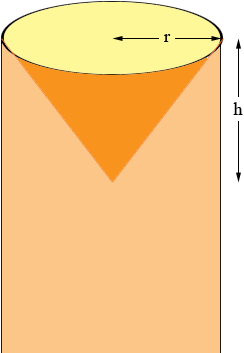
The shape you need to make the cone is a sector of a circle I suggest you look at my response to Amy for details. The radius of the sector you need, the length |PQ| in my diagram is √(276.5² + h²) mm.

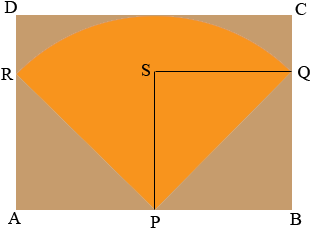
The length of the arc RQ is the circumference of the top of the cone which is 553 × π mm. The measure of the angle RPQ is (180 × 553/|PQ|)^o and hence sin((180 × 553/|PQ|)^o) = |SQ|/|PQ|. Thus |RQ| = 2 |SQ| = 2 |PQ| sin((180 × 553/|PQ|)^o) mm.

Thus you need a rectangle ABCD of plastic with |AB| = 2 |PQ| sin((180 × 553/|PQ|)^o) mm and |BC| = |PQ| mm. From P, the midpoint of the side AB draw an arc of radius |PQ| mm. This will intersect the sides of the rectangle at points R and Q and allow you to cut out the sector.

I would try it on paper first.

Penny