The Pythagorean theorem with triangles rather than squares

HOME

Math Central

Quandaries & Queries

Question from Zachary, a student:

I need to figure out how to prove the pythagorean theorem using equilateral triangles
instead of using square. I know that A^2+B^2=C^2, but how do you get that by using equilateral
triangles. I know the area of a triangle is BH1/2=Area. So what i need to know is how to derive the
formula of a triangle to get the pythagorean theorem

Hi Zachary,

The Pythagorean theorem says that if you have a right angled triangle and you construct a square on each of the sides then the area of the square on the hypotenuse is the sum of the areas of the squares on the other two sides. What is yo construct an equilateral triangle on each side rather than a square? What can yo say about the areas of the three equilateral triangles?

triangles

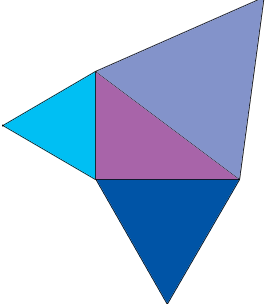
Find an expression for the area of an equilateral triangle in terms of the length of a side. If the sides of the right triangle have lengths A, B and C with the hypotenuse having length C then the Pythagorean theorem states that A² + B² = C². Put this together with the expressions for the areas of the equilateral triangles. What die this tell you about a relationship among the areas of the three equilateral triangles?

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.