Cool idea!

I'm following the same method I used in this earlier answer.

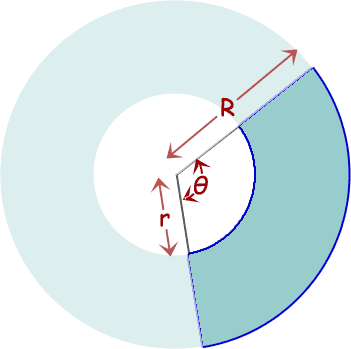
The basic pattern is shown on the right. We need to find the size of the external radius R, the internal radius r, and the central angle size θ.

What we know is that the inner arc length is 32", the outer arc length is 44", and the distance between the circles is 8".

When we cut this pattern out and roll it into the truncated cone, we get the geometry below:

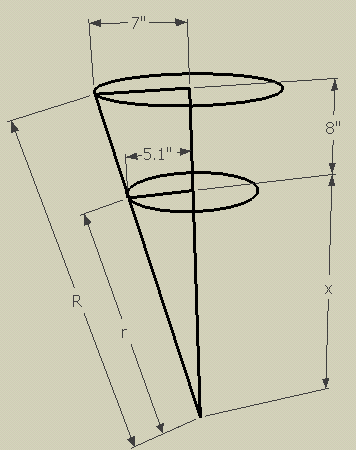
I've noted your radii as 7" and 5.1" (half your diameter measurements of 14" and 10.2").

Do you see the right triangles in the diagram? They are similar triangles, so the ratios of corresponding sides are the same. So we can find the value x:

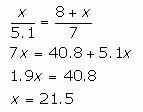
This in turn allows us to calculate the value of r by using Pythagoras' Theorem:

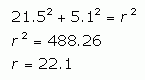
Returning to the similar triangles, we can use this to calculate R:

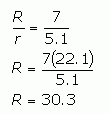
So now all we need to know is the central angle θ.

Since we know the outer radius R is 30.3", the size of the outer circle circumference would by 2π times this. But we want just a portion of the full circumference: the portion that is 44" in length. So the ratio is:

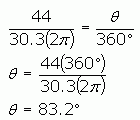
So to make the pattern, make the outer radius 30.3", the inner radius 22.1" and the central angle 83.2 degrees.

Happy Halloween!

Stephen La Rocque.