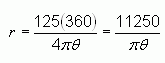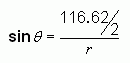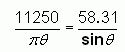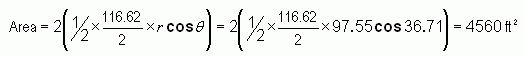Hi Keith.

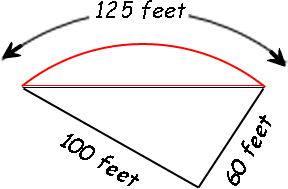
If I understand your description, you have basically this shape:

The volume of this shape is the top area times the depth (3 ft). To calculate the top area, we can split it into a circular segment and a right triangle.

The right triangle is easy enough: its area is half the base times the height.
So ½×100×60 = 3000 square feet. The circular segment is tougher, because we need to know the central angle and the radius to calculate it.

Let's do some trigonometry then. First, we need to know the chord length. That's the hypotenuse of the right triangle, so the chord length c is just the square root of the sum of the squares of the straight sides:

Now let's extend the circular definition and draw this diagram:

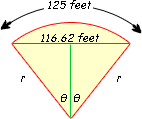
I have drawing radii from the ends of the arc and also bisected the central angle, forming two congruent right triangles inside the figure.

The ratio of the arc length to the circumference of the whole circle must be the same as the central angle of the arc to the angle of the whole circle (360°). This means

Solving this for the radius we get:

Now look at the right triangle inside the diagram. The sine relationship tells us:

And if we solve this for the radius, we get:

So we have two expressions that equal the radius, so they equal each other:

It isn't possible to solve this exactly, so I will use Newton's Method for approximation. That gives me the value of theta = 36.71°. Now I use that in either of the earlier equations to solve for the radius and I find that r = 97.55 feet.

Now I have what I need to calculate the area of the circular segment. I can find the area of the circular sector (the whole yellow pie slice) by taking the proportional of the whole circle's area that corresponds to the angle:

Subtract from that the area of the isosceles triangle (which is really just 2 times the area of the right triangle). For that we need the length of the other leg of the right triangle, which we can get using cosine:

Thus, the area of the circular segment is the difference of these:

Area = 6097 - 4560 = 1537 ft².

Now we add this to the first right triangular area (3000 ft²) to get a total of 4537 ft², that's the area of the surface.

Turn that into the volume by multiplying by the depth of 3 ft and we have 13611 ft³.

That's how much concrete you need. Usually this is shipped in cubic yards rather than cubic feet, so you need to divide by 27 to convert from cubic feet to cubic yards. That makes 504 cubic yards.

Quite a bit of concrete.

Cheers,
Stephen La Rocque.