| |||
| Math Central | Quandaries & Queries |
|
Question from Wayne: I have the actual length of an arc plus the length of the cord. How do I determine the radius of the arc. |
Hi Wayne,
I don't have a nice answer to your question but I'll show you what I can do.
Suppose that the length of the arc is a, the length of the chord is c, the radius of the circle is r and the angle at the centre of the circle subtended by the arc has measure θ radians.
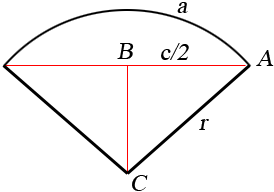
I am going to use two facts. First the length of the arc is given by a = r θ. Secondly since triangle ABC is a right triangle sin(θ/2) = |AB|/|CA| so sin(θ/2) = c/(2r).
From the first equation r = a/θ and substituting this into the second equation yields sin(θ/2) = c θ/(2 a). You know the values of c and a and hence if you can solve this equation for θ you can substitute the value into a = r θ and solve for r.
Unfortunately there is no way to solve sin(θ/2) = c θ/(2 a) for θ. The best I can offer is an approximation method like Newton's Method, described in the answer to a previous problem.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.