| |||
| Math Central | Quandaries & Queries |
|
Question from Malcolm: I am looking for a formula to find the volume of my pond. I know the average surface diameter and the average bottom arc length.(The arc from one bank through a point in the bottom and on to the surface on the other bank. I am not able to get a good measurement of the depth at this time. Can the volume be figured with the known measurements (the cord and the arc)? Thanks: MS |
Malcolm,
You can make an approximation of the volume if you are willing to assume that the surface of the pond is circular and the bottom arcs are also circular. Even with these assumptions the mathematics is not straightforward.
With the circular assumptions the pond can be seen as a slice off a sphere of unknown radius R.
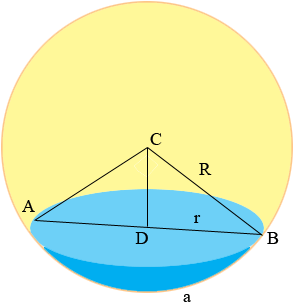
Suppose the diameter of the surface of the pond is d units, r = d/2 and the length of the arc formed by the bottom of the pool is a units. Let the central angle BCA be θ radians. (The expressions are easier in radians than in degrees.) The challenge is to find R for then Pythagoras theorem will allow us to find |CD|, the length of CD and then the depth of the pool, R - |CD|.
The relationship among R, a and θ is that a = R θ. Also from triangle DBC I know that sin(θ/2) = r/R. Putting these two equations together I get
sin(θ/2) = (r/a) θ
You have values for r and a and hence solving this equation for θ will allow you to use a = R θ to find R. Unfortunately there is no way to solve this equation for θ. The best that can be done is to approximate θ. There is some information on solving this equation for θ in our response to an earlier question.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.