Hi Misty. Here's how I would solve this problem. Start by drawing the barn and choosing one corner of the barn to tie the goat to. Then see what area the goat can reach without going around any corners:

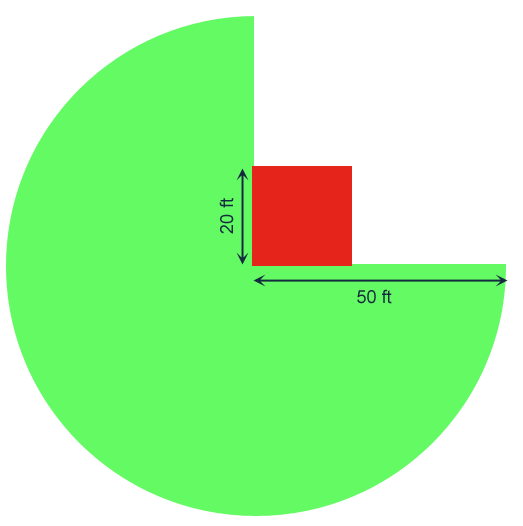
Now if we bend around one corner, we can go further, but 20 ft of rope is strung along the building, so our curves have radii of 30 ft rather than 50 ft:

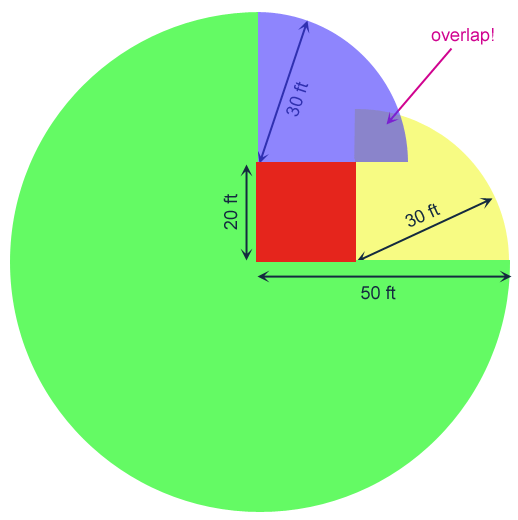
Notice that we have already overlapped. The further 10 ft of rope just goes over (again) area the goat can more easily reach by going around the barn the other way.

The trouble is to find out the area that the blue and yellow quarters surround. Let's re-draw this adding some points and construction lines:

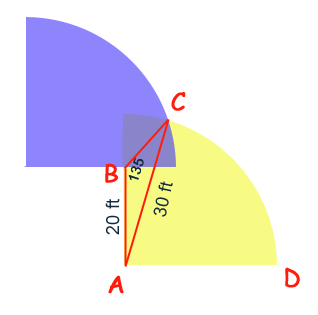
We can use the Law of Sines to solve the unknown angles and sides in triangle ABC:

sin(B) / AC = sin(C) / AB
sin(135) / 30 = sin(C) / 20
sin(C) = (2/3) sin(135)
C = arcsin [ (2/3) sin(135) ]
C = 28.13 degrees.

A = 180 - B - C
A = 180 - 135 - 28.13
A = 16.87 degrees.

sin(A) / BC = sin(B) / AC
sin(16.87) / BC = sin(135) / 30
BC = 30 sin(16.87) / sin(135)
BC = 12.31 ft.

Now that we have this information, we can calculate the area of the triangle, by using Heron's Formula:

S = (AB + BC + AC) / 2
S = (20 + 30 + 12.31) / 2
S = 31.15

Area of triangle = sqrt( S (S - AB) (S - AC) (S - BC) )
Area of triangle = sqrt(31.15 ( 31.15 - 20) ( 31.15 - 8.21) (31.15 - 30) )
Area of triangle = 95.72 square feet.

Next let me add the area of the sector ACD. The angle CAD must be 90 - BAC, so CAD is 90 - 16.87 = 73.13 degrees. Thus sector ACD is 73.13/360 of the full circle of radius 30 feet. That means

Area of sector = (73.13 / 360) π (30)²
Area of sector = 574.36 square feet.

If I add these two areas together, I get the area of shape ABCD: 95.72 + 574.36 = 670.08 square feet.

Can you finish the problem? Take a look at the symmetry to complete it.

Cheers,
Stephen La Rocque.