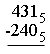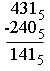Hi Nikki,

If you are using base five notation to express numbers then the only symbols you have for digits are 0, 1, 2, 3, and 4. Thus 51 can't be a base five number.

You should first look at my note to Jana on adding using base five notation. Subtraction is straightforward of you are always subtracting a smaller digit from a larger digit. The challenge is to deal with borrowing. Let's look at a base 10 problem first.

Starting in the first column 6 - 3 = 3 but in the next column you need to borrow from the third column. Since this is base ten notation you are borrowing ten so the 6 in the third column becomes 5 and adding ten to 3 you have thirteen in the second column.

5 from 13 is 8 and 4 from 5 is 1 so the result is

Now let's try a base 5 problem.

As in the base ten problem the first column is easy, 1 - 0 = 1. In the second column you need to borrow from the third column. Since the numbers are written in base five notation you are borrowing five so the 4 in the third column becomes 3 and adding five to 3 gives you eight in the second column.

4 from eight is 4 and 2 from 3 is 1 so the result is

You should check your answer by adding 141₅ and 240₅ to ensure you get 431₅.

Harley