Hi,

In many situations with complex numbers, especially when dealing with powers, it is helpful to express the numbers in exponential form. That is express the number as r e^iθ = r(cos(θ) + i sin(θ)) where θ is expressed in radians. To do this I usually think of the geometric representation of the number in the complex plane. Using this technique the number i can be written

i = e^iπ/2.

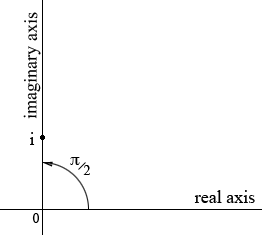
Thus

iⁱ = (e^iπ/2)ⁱ = e^i2π/2 = e^-π/2

Thus iⁱ is a real number! In decimal form it is approximately 0.207880.

Here is a more algebraic way to see it. De Moivre showed that e^ix = cosx + isinx so that e^iπ/2 = cos(π/2) + isin(π/2) = i, for example. Thus to look at iⁱ one could consider iⁱ = (e^iπ/2)ⁱ and that's the same as e^(iπ/2)i = e^(i2)(π/2) = e^-π/2.

Penny

Hi,

Since sine and cosine are periodic with period 2π, for any integer n

e^{i(2nπ +π/2)} = cos(π/2 + 2nπ) + isin(π/2 + 2nπ) = cos(π/2) + isin(π/2) = i

Hence iⁱ has infinitely many values, e^{2nπ -π/2} for n any integer. The valuse closest unity being approximately

(..., 0.0003882, 0.2079, 111.32, 59609, ...)

RD