| |||
| Math Central | Quandaries & Queries |
|
Question from Steven: I am trying to layout a large raduis between 2 points in a building and |
Steven sent us this diagram
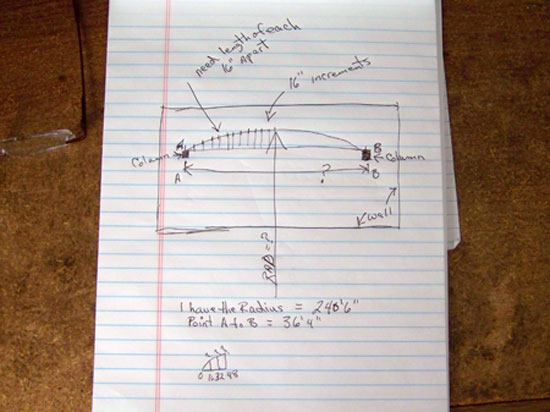
Hi Steven. Thanks for sending us the diagram - that clarifies things quite a bit. I note that the radius in your diagram is 240'6" whereas in your earlier message you said 187'6", so I presume the diagram (240'6") has the correct value.
This is a lot like a problem I solved in 2007 here: http://mathcentral.uregina.ca/QQ/database/QQ.09.06/s/angela1.html
On that web page, I showed how to derive a general solution. We can use the results of that work to speed us to our goal. First though, I should notify you that the curvature is very slight: a chord of length 34'8" is tiny compared to the radius of 240'6", so the maximum height of the arch is going be be very small as well - if this isn't at all what you were expecting, then review whether your radius is really that large.
Okay, to begin, we calculate the apothem using Pythagoras. That is, if you draw a line connecting the midpoint of the chord (the flat base of the arch) to the center of the circle and connect the endpoint of the chord to the center as well, then you have constructed a right angle triangle. We know the hypotenuse is the radius (240.5 feet) and the short side is half the chord length, which makes 17.33333 feet. The long leg is the apothem (I'll call it A) and can be found using Pythagoras:
240.52 = 17.3333332 + A2
A = √(240.522 - 17.333332 ) = 239.8746 feet.
Thus for my formulae on the other web page, we have x0 = 17.33333 feet, y0 is -239.8746 feet and r2 = 240.52 = 57840.25 square feet.
I'll convert from feet to inches, so now x0 = 208 inches, y0 is -2878.5 inches and r2 = 8328996 square inches.
Okay, so now we can compute the heights at 16 inch intervals starting at one end.
Thus, starting from one column and moving away at 16 inch intervals (the x co-ordinate), we have the following heights (y co-ordinate) in inches:
| x (inches from left column) | y (inches from ground) y = y0 + √(r2 - (x - x0 )2 ) |
|---|---|
| 0 | 0 |
| 16 | 1.11 |
| 32 | 2.13 |
| 48 | 3.07 |
| 64 | 3.91 |
| 80 | 4.66 |
| 96 | 5.33 |
| 112 | 5.91 |
| 128 | 6.4 |
| 144 | 6.8 |
| 160 | 7.11 |
| 176 | 7.33 |
| 192 | 7.46 |
| 208 | 7.5 |
| 224 | 7.46 |
| 240 | 7.33 |
| 256 | 7.11 |
| 272 | 6.8 |
| 288 | 6.4 |
| 304 | 5.91 |
| 320 | 5.33 |
| 336 | 4.66 |
| 352 | 3.91 |
| 368 | 3.07 |
| 384 | 2.13 |
| 400 | 1.11 |
| 416 | 0 |
As you can see, the height at the columns is 0 inches (as expected) and the height in the center is 7.5 inches. That's a very slight arch, but hopefully it is what you are seeking.
Cheers,
Stephen La Rocque.
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.