Hi Wanda,

The question was

What is the area of an equilateral triangle inscribed in a circle whose circumference is 6 pi?

I copied the diagram from my response in 2007, added one label, a line and changed the colouring.

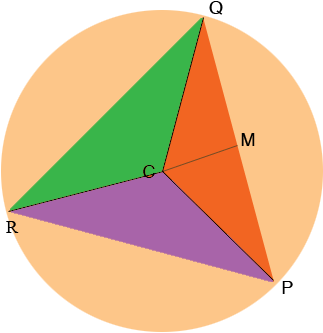
As you can see the triangle PQR is partitioned into three congruent triangles PQC, QRC and RPC. I am going to find the area of triangle PQC and multiply by 3 to determine the area of triangle PQR.

To find the area of triangle PQC I cut it along the line MC and move the bottom half so that the line segment PM lies along QM. Since M is the midpoint of PQ these line segments will match.

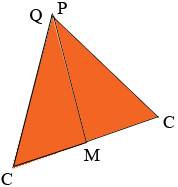
The labeling on this diagram is confusing since there are two points with the label C and one point with two labels P and Q o I am going to erase the label P and one of the Cs.

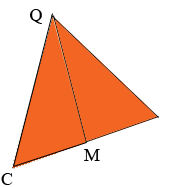
The area of this triangle is the same as the area of triangle QCP in the original diagram.

In my previous response I argued that measure of the angle QCM is 60^o and a similar argument shows angle MCP also has a measure of 60^o. Since the sum of the angles of a triangle 1s 180^o the triangle above is an equilateral triangle. We know that QC is a radius of the circle so |QC| = 3 and thus |CM| = 3/2 = 1 1/2. This is half the base of the triangle above and hence to determine its area (and hence the area of triangle QCP) I only need to find its height |MQ|. For this we can use Pythagoras theorem.

Triangle QCM is a right triangle so

|CM|² + |MQ|² = |QC|²

or

(3/2)² + |MQ|² =3²

and thus |MQ| = 3 √3/2.

Finally the area of triangle PQR is

3 × (3/2) × (3 √3/2) = 27 √3/4 square units.

I hope this helps,
Penny