Hi Bahra,

You find the x and y intercepts of any type of graph by the same procedure. The definition of an intercept is a point that lies on either the x-axis (x-intercept or sometimes called zero of the function) or the y-axis. Since all along the x-axis, y equals 0, we can use this fact to find the x-intercept. Similarly, all along the y-axis, x equals 0 so we can find the y-intercept. Let's look at a similar rational function y=6/(x-4)

To find the y intercept, we set x=0 so then y=6/-4=-1.5 so the point is (0,-1.5)

To find the x intercept, we set y=0 so 0=6/(x-4). Since the only way a fraction can equal 0 is if the numerator is 0. Since there is no way for 0=6, we can say that there is no x-intercept (or the graph does not cross the x-axis).

Determining the vertical asymptote is a way to represent x-values where the graph cannot exist. Since we have a rational function, we know if the denominator equals 0 then the fraction is undefined. So to find the vertical asymptote(s) we set the denominator equal to 0 and solve. So in the case of our example

0=x-4

This means there is a vertical asymptote at x=4

Determining the horizontal asymptote or slant asymptote is a little trickier. First a couple of definitions that you need to know to understand the rules to determine the situation:

Degree of a function is the largest exponent attached to a variable. The number in front of the variable with the largest exponent is called the leading coefficient.

Rules for Determining horizontal or slant asymptotes of rational functions

1. If the degree in the denominator is larger than the degree in numerator then the horizontal asymptote is y=0. In our example y=6/(x-4). Since there is no x in the numerator the degree is 0. In the denominator the degree is 1. Since the degree is larger in the denominator then we know that the horizontal asymptote is y=0.

2. If the degree in the denominator and the degree in numerator are the same then the horizontal asymptote is a ratio of the leading coefficients. If for example you wanted to find the the horizontal asymptote of y=(4x-5)/(3x-4) we look at the numbers in front of the variable with the biggest exponent in the numerator and denominator then divide them. In this case the horizontal asymptote would be y=4/3.

3. If the degree in the denominator is smaller than the degree in numerator then there is no horizontal asymptote but a slant asymptote. The equation of the slant asymptote can be found using polynomial long division or synthetic division, ignoring any remainders.

The last step is always determining what parts of the function are above or below the x-axis by the information we know about the x-axis. We know there is no x-intercept but we know there is a vertical asymptote at x=4. So lets figure out what is happening on either side of x=4.

When x is less than 4, say x=0 then y=-1.5. So we know for all values of x less than 4, y will be negative (or the graph is below the x-axis).

When x is greater than 4, say x=5 then y=6. so we know for all values of x greater than 4, y will be positive (or the graph is above the x-axis).

If you put all the information together for our example of y=6/(x-4) we get the following graph:

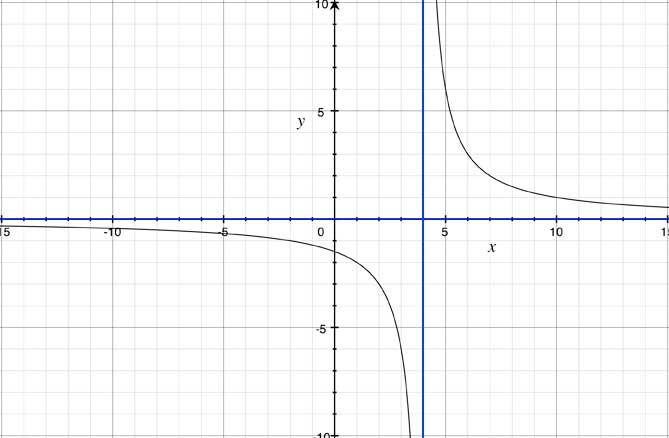
Hope this helps,

Janice