| |||
| Math Central | Quandaries & Queries |
|
Question from Aye, a student: Hello, Can you please help me with this problem, I cannot seem to find the correct method of solving, not sure how to draw the points A, B, and T and solve the scalene triangle with what is given. Can you please explain the desired Figure and some hints about the solution!! Thank you so much, Aye ! The Problem is as follows: In order to decide the height of a remote mountain peak T one measures from two points A and B the angles u and v where the lines AT and BT made with the Horizontal plane respectively. From B, which lies 2400 m from A, one can see A and T by the same point of the compass. Find the height of a mountain peak, if A and B are known to be 950 m and 875 m above sea level respectively, as well as u = 43,8 degree and v = 25,2 degree. |
Aye,
In my diagram the blue bar at the bottom marks sea level and the height of the mountain is h m above sea level
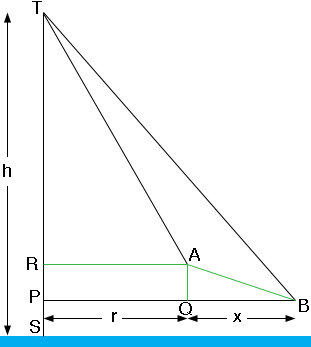
Triangle AQB is a right triangle, |AQ| = 950 - 875 = 75 m and |AB| = 2400 m. Thus you can use Pythagoras' theorem to find the distance x = |QB|. Now your situation is very similar to the problem we received from Brina a while ago. You can proceed as Stephen did to solve Brina's problem using triangles TRA and TPB. In Stephen's solution the two triangles had the same height but in your problem the triangles have heights h - |RS| m and h - |PS| m respectively. But you know |RS| and |PS| so Stephen's technique should work for you.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.