| |||
| Math Central | Quandaries & Queries |
|
Question from Darryl: Is there a formula to determine the chord length of an arc knowing only the arc length and the arc depth (sagitta)? I know you can't find the radius with only these two inputs, but can you find the chord length?
|
Darryl,
If you know the arc length of a circular arc and the sagitta you can write down an expression for the radius, but unfortunately there is no nice way to solve this expression for the radius. The best you can do is approximate the radius by using something like Newton's method. Look for example at the response to this question that Stephen and I gave to Ned.
If you could determine the chord length, c = |AB| in the diagram below then, since triangle DCB is a right triangle, Pythagoras theorem would give you
(c/2)2 + (r - s)2 = r2.
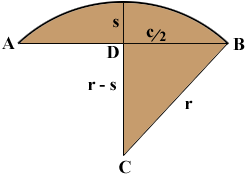
Solving this equation for r yields
r = (4s2 + c2)/(8s).
Hence if you could find the chord length directly from the arc length and the sagitta then you could calculate the radius without the need of an approximation. I doubt very much that this is possible.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.